P
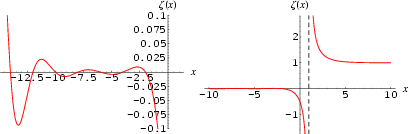
The Riemann zeta function is an extremely important special function of mathematics and physics that arises in definite integration and is intimately related with very deep results surrounding the prime number theorem. While many of the properties of this function have been investigated, there remain important fundamental conjectures (most notably the Riemann hypothesis) that remain unproved to this day. The Riemann zeta function ![]() is defined over the complex plane for one complex variable, and is conventionally denoted s (instead of the usual z) in deference to the notation used by Riemann in his 1859 paper that founded the study of this function (Riemann 1859). It is implemented in Mathematica as Zeta[s].
is defined over the complex plane for one complex variable, and is conventionally denoted s (instead of the usual z) in deference to the notation used by Riemann in his 1859 paper that founded the study of this function (Riemann 1859). It is implemented in Mathematica as Zeta[s].
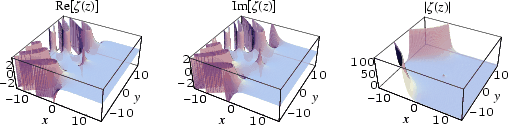
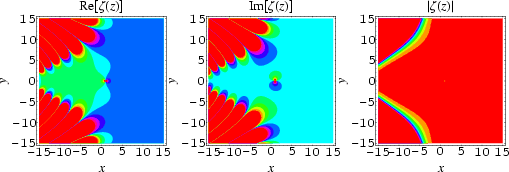
The plot above shows the "ridges" of ![]() for
for ![]() and
and ![]() .
.
On the real line with x > 1, the Riemann zeta function can be defined by the integral
| (1) |
where ![]() is the gamma function. If x is an integer n, then we have the identity
is the gamma function. If x is an integer n, then we have the identity
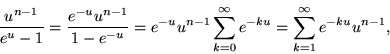 |
(2) |
so
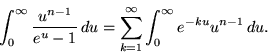 |
(3) |
To evaluate ![]() ,
,![]() so that
so that ![]() and plug in the above identity to obtain
and plug in the above identity to obtain
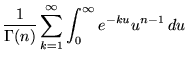 |
(4) | ||
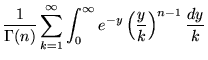 |
(5) | ||
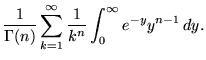 |
(6) |
Integrating the final expression in (6) gives
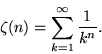 |
(7) |
The Riemann zeta function can also be defined in terms of multiple integrals by
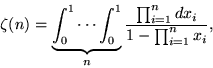 |
(8) |
and as a Mellin transform by
| (9) |
for ![]() ,
,![]() is the fractional part (Balazard and Saias 2000).
is the fractional part (Balazard and Saias 2000).
Note that the zeta function has a singularity at n = 1, where it reduces to the divergent harmonic series.
The Riemann zeta function satisfies the reflection functional equation
| (10) |
(Hardy 1999, p. 14; Krantz 1999, p. 160), a similar form of which was conjectured by Euler for real s (Euler, read in 1749, published in 1768; Ayoub 1974; Havil 2003, p. 193). A symmetrical form of this functional equation is given by
| (11) |
(Ayoub 1974), which was proved by Riemann for all complex s (Riemann 1859).
As defined above, the zeta function ![]() with
with ![]() a complex number is defined for
a complex number is defined for ![]() .
.![]() has a unique analytic continuation to the entire complex plane, excluding the point s = 1, which corresponds to a simple pole with complex residue 1 (Krantz 1999, p. 160). In particular, as
has a unique analytic continuation to the entire complex plane, excluding the point s = 1, which corresponds to a simple pole with complex residue 1 (Krantz 1999, p. 160). In particular, as ![]() ,
,![]() obeys
obeys
| (12) |
where ![]() is the Euler-Mascheroni constant (Whittaker and Watson 1990, p. 271).
is the Euler-Mascheroni constant (Whittaker and Watson 1990, p. 271).
To perform the analytic continuation for ![]() ,
,
 |
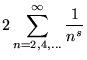 |
(13) | |
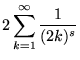 |
(14) | ||
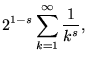 |
(15) |
so rewriting in terms of
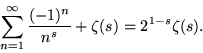 |
(16) |
Therefore,
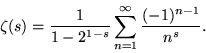 |
(17) |
Here, the sum on the right-hand side is exactly the Dirichlet eta function ![]() (sometimes also called the alternating zeta function). While this formula defines
(sometimes also called the alternating zeta function). While this formula defines ![]() for only the right half-plane
for only the right half-plane ![]() ,
,![]() to the entire complex plane except s = 1) is given by
to the entire complex plane except s = 1) is given by
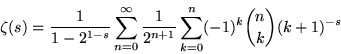 |
(18) |
(Havil 2003, p. 206), where ![]() is a binomial coefficient, which was conjectured by Knopp around 1930, proved by Hasse (1930), and rediscovered by Sondow (1994). This equation is related to renormalization and random variates (Biane et al. 2001) and can be derived by applying Euler's series transformation with n = 0 to equation (17).
is a binomial coefficient, which was conjectured by Knopp around 1930, proved by Hasse (1930), and rediscovered by Sondow (1994). This equation is related to renormalization and random variates (Biane et al. 2001) and can be derived by applying Euler's series transformation with n = 0 to equation (17).
Hasse (1930) also proved the related globally (but more slowly) convergent series
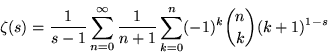 |
(19) |
that, unlike (18), can also be extended to a generalization of the Riemann zeta function known as the Hurwitz zeta function ![]() .
.![]() is defined such that
is defined such that
| (20) |
(If the singular term is excluded from the sum definition of ![]() ,
,![]() as well.) Expanding
as well.) Expanding ![]() about s = 1 gives
about s = 1 gives
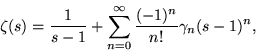 |
(21) |
where ![]() are the so-called Stieltjes constants.
are the so-called Stieltjes constants.
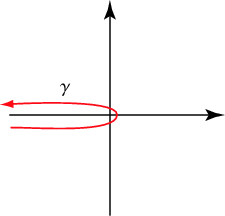
The Riemann zeta function can also be defined in the complex plane by the contour integral
| (22) |
for all ![]() ,
,
Zeros of ![]() come in (at least) two different types. So-called "trivial zeros" occur at all negative even integers s = -2, -4, -6, ..., and "nontrivial zeros" at certain
come in (at least) two different types. So-called "trivial zeros" occur at all negative even integers s = -2, -4, -6, ..., and "nontrivial zeros" at certain
| (23) |
for s in the "critical strip" ![]() .
.![]() all have real part
all have real part ![]() ,
,![]() roots.
roots.
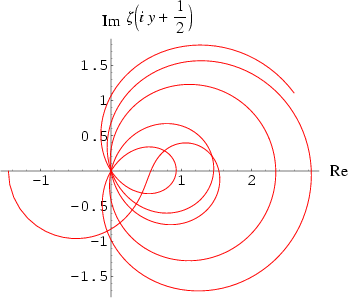
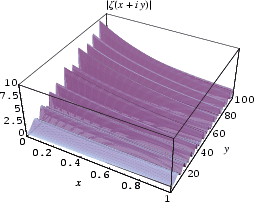
The plot above shows the real and imaginary parts of ![]() (i.e., values of
(i.e., values of ![]() along the critical strip) and y is varied from 0 to 35 (Derbyshire 2004, p. 221).
along the critical strip) and y is varied from 0 to 35 (Derbyshire 2004, p. 221).
The Riemann zeta function can be split up into
| (24) |
where Z(t) and ![]() are the Riemann-Siegel functions. The Riemann zeta function is related to the Dirichlet lambda function
are the Riemann-Siegel functions. The Riemann zeta function is related to the Dirichlet lambda function ![]() and Dirichlet eta function
and Dirichlet eta function ![]() by
by
| (25) |
and
| (26) |
(Spanier and Oldham 1987). It is related to the Liouville function ![]() by
by
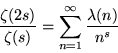 |
(27) |
(Lehman 1960, Hardy and Wright 1979). Furthermore,
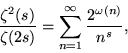 |
(28) |
where ![]() is the number of distinct prime factors of n (Hardy and Wright 1979, p. 254).
is the number of distinct prime factors of n (Hardy and Wright 1979, p. 254).
The derivative of the Riemann zeta function for ![]() is defined by
is defined by
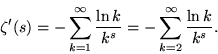 |
(29) |
Using equation (18) gives the special case
| (30) |
which can be derived directly from the Wallis formula (Sondow 1994). In general, ![]() can be expressed analytically in terms of
can be expressed analytically in terms of ![]() ,
,![]() ,
,![]() ,
,![]() ,
,
| (31) | |||
| (32) |
The series for ![]() about s = 1 is
about s = 1 is
| (33) |
where ![]() are Stieltjes constants.
are Stieltjes constants.
In 1739, Euler found the rational coefficients C in ![]() in terms of the Bernoulli numbers. Which, when combined with the 1882 proof by Lindemann that
in terms of the Bernoulli numbers. Which, when combined with the 1882 proof by Lindemann that ![]() is transcendental, effectively proves that
is transcendental, effectively proves that ![]() is transcendental. The study of
is transcendental. The study of ![]() is significantly more difficult. Apéry (1979) finally proved
is significantly more difficult. Apéry (1979) finally proved ![]() to be irrational, but no similar results are known for other odd n. As a result of Apéry's important discovery,
to be irrational, but no similar results are known for other odd n. As a result of Apéry's important discovery, ![]() is sometimes called Apéry's constant. Rivoal (2000) and Ball and Rivoal (2001) proved that there are infinitely many integers n such that
is sometimes called Apéry's constant. Rivoal (2000) and Ball and Rivoal (2001) proved that there are infinitely many integers n such that ![]() is irrational, and subsequently that at least one of
is irrational, and subsequently that at least one of ![]() ,
,![]() ,
,![]() is irrational (Rivoal 2001). This result was subsequently tightened by Zudilin (2001), who showed that one of
is irrational (Rivoal 2001). This result was subsequently tightened by Zudilin (2001), who showed that one of ![]() ,
,![]() ,
,![]() ,
,![]() is irrational.
is irrational.
A number of interesting sums for ![]() ,
,
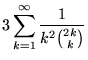 |
(34) | ||
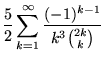 |
(35) | ||
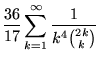 |
(36) |
(Guy 1994, p. 257). Apéry arrived at his result with the aid of the
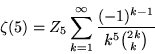 |
(37) |
has been searched for with ![]() a rational or algebraic number, but if
a rational or algebraic number, but if ![]() is a root of a polynomial of degree 25 or less, then the Euclidean norm of the coefficients must be larger than
is a root of a polynomial of degree 25 or less, then the Euclidean norm of the coefficients must be larger than ![]() (Bailey and Plouffe). Therefore, no such sums for
(Bailey and Plouffe). Therefore, no such sums for ![]() are known for
are known for ![]() .
.
The Riemann zeta function may be computed analytically for even n using either contour integration or Parseval's theorem with the appropriate Fourier series. An unexpected and important formula involving the product of primes was first discovered by Euler ![]() in 1737,
in 1737,
| |
(38) |
| |
(39) |
| |
(40) |
| |
(41) |
Here, each subsequent multiplication by the nth prime ![]() leaves only terms that are powers of
leaves only terms that are powers of ![]() .
.
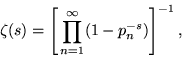 |
(42) |
which is known as the Euler product formula (Hardy 1999, p. 18; Krantz 1999, p. 159), and called "the golden key" by Derbyshire (2004, pp. 104-106). The formula can also be written
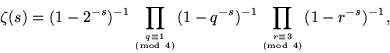 |
(43) |
where q and r are the primes congruent to 1 and 3 modulo 4, respectively.
For even ![]() ,
,
| (44) |
where ![]() is a Bernoulli number (Mathews and Walker 1964, pp. 50-53; Havil 2003, p. 194). Another intimate connection with the Bernoulli numbers is provided by
is a Bernoulli number (Mathews and Walker 1964, pp. 50-53; Havil 2003, p. 194). Another intimate connection with the Bernoulli numbers is provided by
| (45) |
for ![]() ,
,
| (46) |
for ![]() .
.![]() trivially for odd n.) Rewriting (46),
trivially for odd n.) Rewriting (46),
| (47) |
for n = 1, 3, ... (Havil 2003, p. 194), where ![]() is a Bernoulli number, the first few values of which are
is a Bernoulli number, the first few values of which are ![]() ,
,![]() ,
,
Although no analytic form for ![]() is known for odd n,
is known for odd n,
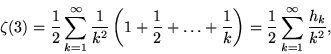 |
(48) |
where ![]() is a harmonic number (Stark 1974). In addition,
is a harmonic number (Stark 1974). In addition, ![]() can be expressed as the sum limit
can be expressed as the sum limit
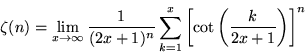 |
(49) |
for n = 3, 5, ... (Apostol 1973, given incorrectly in Stark 1974).
For ![]() the Möbius function,
the Möbius function,
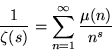 |
(50) |
(Havil 2003, p. 209).
The values of ![]() for small positive integer values of n are
for small positive integer values of n are
| (51) | |||
| (52) | |||
| (53) | |||
| (54) | |||
| (55) | |||
| (56) | |||
| (57) | |||
| (58) | |||
| (59) | |||
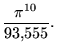 |
(60) |
Euler
An integral for even n is given by
| (61) |
and integrals for odd n are given by
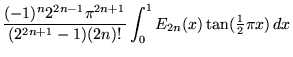 |
(62) | ||
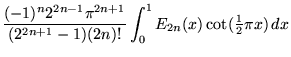 |
(63) | ||
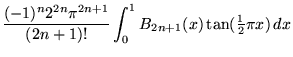 |
(64) | ||
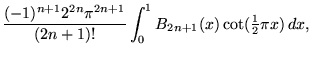 |
(65) |
where
The value of ![]() can be computed by performing the inner sum in equation (18) with s = 0,
can be computed by performing the inner sum in equation (18) with s = 0,
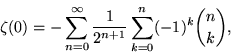 |
(66) |
to obtain
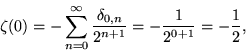 |
(67) |
where ![]() is the Kronecker delta. Similarly, the value of
is the Kronecker delta. Similarly, the value of ![]() can be computed by performing the inner sum in equation (18) with s = -1,
can be computed by performing the inner sum in equation (18) with s = -1,
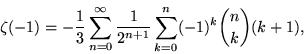 |
(68) |
which gives
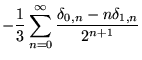 |
(69) | ||
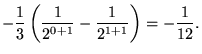 |
(70) |
This value is related to a deep result in renormalization theory (Elizalde et al. 1994, Elizalde 1995, Bloch 1996, Lepowski 1999).
Rapidly converging series for ![]() for n odd were first discovered by Ramanujan (Zucker 1979, Zucker 1984, Berndt 1988, Bailey et al. 1997, Cohen 2000). For n > 1 and
for n odd were first discovered by Ramanujan (Zucker 1979, Zucker 1984, Berndt 1988, Bailey et al. 1997, Cohen 2000). For n > 1 and ![]() ,
,
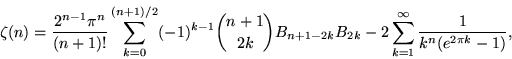 |
(71) |
where ![]() is again a Bernoulli number and
is again a Bernoulli number and ![]() is a binomial coefficient. The values of the left-hand sums (divided by
is a binomial coefficient. The values of the left-hand sums (divided by ![]() ) in (71) for n = 3, 7, 11, ... are 7/180, 19/56700, 1453/425675250, 13687/390769879500, 7708537/21438612514068750, ... (Sloane's A057866 and A057867). For
) in (71) for n = 3, 7, 11, ... are 7/180, 19/56700, 1453/425675250, 13687/390769879500, 7708537/21438612514068750, ... (Sloane's A057866 and A057867). For ![]() and
and ![]() ,
,
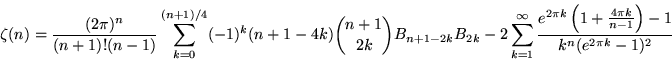 |
(72) |
(Cohen 2000).
Defining
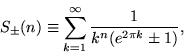 |
(73) |
the first few values can then be written
| (74) | |||
| (75) | |||
| (76) | |||
| (77) | |||
| (78) | |||
| (79) | |||
| (80) | |||
| (81) | |||
| (82) | |||
| (83) |
(Plouffe).
A number of sum identities involving ![]() include
include
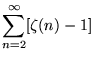 |
(84) | ||
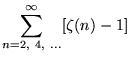 |
(85) | ||
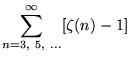 |
(86) | ||
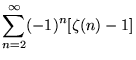 |
(87) |
A surprising sum involving
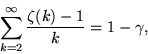 |
(88) |
where ![]() is the Euler-Mascheroni constant (Havil 2003, pp. 109 and 111-112). Other unexpected sums are
is the Euler-Mascheroni constant (Havil 2003, pp. 109 and 111-112). Other unexpected sums are
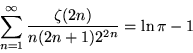 |
(89) |
(Tyler and Chernhoff 1985; Boros and Moll 2004, p. 248) and
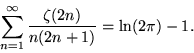 |
(90) |
(89) is a special case of
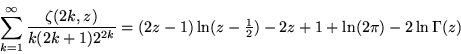 |
(91) |
(Danese 1967; Boros and Moll 2004, p. 248).
An additional set of sums over ![]() is given by
is given by
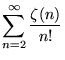 |
(92) | ||
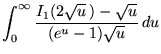 |
(93) | ||
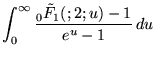 |
(94) | ||
| (95) | |||
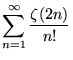 |
(96) | ||
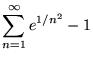 |
(97) | ||
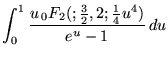 |
(98) | ||
| (99) | |||
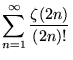 |
(100) | ||
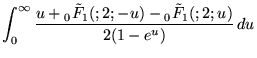 |
(101) | ||
| (102) |
(Sloane's A093720, A076813, and A093721), where
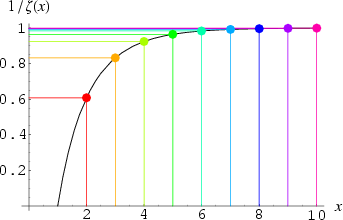
The inverse of the Riemann zeta function ![]() ,
,![]() of pth-powerfree numbers
of pth-powerfree numbers ![]() for several values of n.
for several values of n.
| p | |||||||
| 2 | 0.607927 | 7 | 61 | 608 | 6083 | 60794 | 607926 |
| 3 | 0.831907 | 9 | 85 | 833 | 8319 | 83190 | 831910 |
| 4 | 0.923938 | 10 | 93 | 925 | 9240 | 92395 | 923939 |
| 5 | 0.964387 | 10 | 97 | 965 | 9645 | 96440 | 964388 |
| 6 | 0.982953 | 10 | 99 | 984 | 9831 | 98297 | 982954 |
![]()
Abel's Functional Equation, Berry Conjecture, Critical Line, Critical Strip, Debye Functions, Dirichlet Beta Function, Dirichlet Eta Function, Dirichlet Lambda Function, Euler Product, Harmonic Series, Hurwitz Zeta Function, Khinchin's Constant, Lehmer's Phenomenon, Montgomery's Pair Correlation Conjecture, Periodic Zeta Function, Prime Number Theorem, Psi Function, Riemann Hypothesis, Riemann P-Series, Riemann-Siegel Functions, Riemann-von Mangoldt Formula, Riemann Zeta Function Zeta(2), Riemann Zeta Function Zeros, Stieltjes Constants, Voronin Universality Theorem, Xi-Function
![]()
![]()
Abramowitz, M. and Stegun, I. A. (Eds.). "Riemann Zeta Function and Other Sums of Reciprocal Powers." §23.2 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 807-808, 1972.
Adamchik, V. S. and Srivastava, H. M. "Some Series of the Zeta and Related Functions." Analysis 18, 131-144, 1998.
![]() Aizenberg, L.; Adamchik, V.; and Levit, V. E. "Approaching the Riemann Hypothesis with Mathematica." http://library.wolfram.com/infocenter/Articles/3268/.
Aizenberg, L.; Adamchik, V.; and Levit, V. E. "Approaching the Riemann Hypothesis with Mathematica." http://library.wolfram.com/infocenter/Articles/3268/.
Apéry, R. "Irrationalité de ![]() et
et ![]() .
.
Apostol, T. M. "Another Elementary Proof of Euler's Formula for ![]() .
.
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 332-335, 1985.
Ayoub, R. "Euler and the Zeta Function." Amer. Math. Monthly 81, 1067-1086, 1974.
Bailey, D. H. "Multiprecision Translation and Execution of Fortran Programs." ACM Trans. Math. Software. To appear.
Bailey, D. and Plouffe, S. "Recognizing Numerical Constants." http://www.cecm.sfu.ca/organics/papers/bailey/.
Bailey, D. H.; Borwein, J. M.; and Crandall, R. E. "On the Khinchin Constant." Math. Comput. 66, 417-431, 1997.
Balazard, M. and Saias, E. "The Nyman-Beurling Equivalent Form for the Riemann Hypothesis." Expos. Math. 18, 131-138, 2000.
Balazard, M.; Saias, E.; and Yor, M. "Notes sur la fonction ![]() de Riemann, 2." Adv. Math. 143, 284-287, 1999.
de Riemann, 2." Adv. Math. 143, 284-287, 1999.
Ball, K. and Rivoal, T. "Irrationalité d'une infinité valeurs de la fonction zêta aux entiers impairs." Invent. Math. 146, 193-207, 2001.
Berndt, B. C. Ch. 14 in Ramanujan's Notebooks, Part II. New York: Springer-Verlag, 1988.
Biane, P.; Pitman, J.; and Yor, M. "Probability Laws Related to the Jacobi Theta and Riemann Zeta Functions, and Brownian Excursions." Bull. Amer. Math. Soc. 38, 435-465, 2001.
Bloch, S. "Zeta Values and Differential Operators on the Circle." J. Algebra 182, 476-500, 1996.
Boros, G. and Moll, V. Irresistible Integrals: Symbolics, Analysis and Experiments in the Evaluation of Integrals. Cambridge, England: Cambridge University Press, 2004.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Natick, MA: A. K. Peters, pp. 95-96 and 99-100, 2003.
Borwein, D. and Borwein, J. "On an Intriguing Integral and Some Series Related to ![]() .
.
Borwein, J. M.; Bradley, D. M.; and Crandall, R. E. "Computational Strategies for the Riemann Zeta Function." J. Comput. Appl. Math. 121, 247-296, 2000.
Castellanos, D. "The Ubiquitous Pi. Part I." Math. Mag. 61, 67-98, 1988.
Choudhury, B. K. "The Riemann Zeta-Function and Its Derivatives." Proc. Roy. Soc. London Ser. A 450, 477-499, 1995.
Cohen, H. "High Precision Computation of Hardy-Littlewood Constants." Preprint. http://www.math.u-bordeaux.fr/~cohen/hardylw.dvi.
Conrey, J. B. "The Riemann Hypothesis." Not. Amer. Math. Soc. 50, 341-353, 2003. http://www.ams.org/notices/200303/fea-conrey-web.pdf.
Cvijovic, D. and Klinowski, J. "Integral Representations of the Riemann Zeta Function for Odd-Integer Arguments." J. Comput. Appl. Math. 142, 435-439, 2002.
Danese, A. E. "Solution to Problem 1801. A Zeta-Function Identity." Amer. Math. Monthly 74, 80-81, 1967.
Davenport, H. Multiplicative Number Theory, 2nd ed. New York: Springer-Verlag, 1980.
Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, 2004.
Edwards, H. M. Riemann's Zeta Function. New York: Academic Press, 1974.
Elizalde, E. Ten Physical Applications of Spectral Zeta Functions. Berlin: Springer-Verlag, 1995.
Elizalde, E.; Odintsov, S. D.; Romeo, A.; Bytsenko, A. A.; and Zerbini, S. Zeta Regularization Techniques With Applications. River Edge, NJ: World Scientific, 1994.
Euler, L. "Remarques sur un beau rapport entre les series des puissances tant directes que réciproques." Mémoires de l'academie des sciences de Berlin 17, 83-106, 1768. Reprinted in Opera Omnia, Series 1, Vol. 15, pp. 70-90.
Guy, R. K. "Series Associated with the ![]() -Function." §F17 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 257-258, 1994.
-Function." §F17 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 257-258, 1994.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Hardy, G. H. and Wright, E. M. "The Zeta Function." §17.2 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 245-247 and 255, 1979.
Hasse, H. "Ein Summierungsverfahren für die Riemannsche Zeta-Reihe." Math. Z. 32, 458-464, 1930.
Hauss, M. Verallgemeinerte Stirling, Bernoulli und Euler Zahlen, deren Anwendungen und schnell konvergente Reihen für Zeta Funktionen. Aachen, Germany: Verlag Shaker, 1995.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.
Howson, A. G. "Addendum to: 'Euler and the Zeta Function' (Amer. Math. Monthly 81 (1974), 1067-1086) by Raymond Ayoub." Amer. Math. Monthly 82, 737, 1975.
Ivic, A. A. The Riemann Zeta-Function. New York: Wiley, 1985.
Ivic, A. A. Lectures on Mean Values of the Riemann Zeta Function. Berlin: Springer-Verlag, 1991.
Jones, G. A. and Jones, J. M. "The Riemann Zeta Function." Ch. 9 in Elementary Number Theory. Berlin: Springer-Verlag, pp. 163-189, 1998.
Karatsuba, A. A. and Voronin, S. M. The Riemann Zeta-Function. Hawthorne, NY: De Gruyter, 1992.
Katayama, K. "On Ramanujan's Formula for Values of Riemann Zeta-Function at Positive Odd Integers." Acta Math. 22, 149-155, 1973.
Keiper, J. "The Zeta Function of Riemann." Mathematica Educ. Res. 4, 5-7, 1995.
Knopp, K. "4th Example: The Riemann ![]() -Function." Theory of Functions Parts I and II, Two Volumes Bound as One, Part II. New York: Dover, pp. 51-57, 1996.
-Function." Theory of Functions Parts I and II, Two Volumes Bound as One, Part II. New York: Dover, pp. 51-57, 1996.
Krantz, S. G. "Riemann's Zeta Function." §13.2 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 158-159, 1999.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 35, 1983.
Lehman, R. S. "On Liouville's Function." Math. Comput. 14, 311-320, 1960.
Lepowski, J. "Vertex Operator Algebras and the Zeta Function." 29 Sep 1999. http://arxiv.org/abs/math.QA/9909178/.
Mathews, J. and Walker, R. L. Mathematical Methods of Physics, 2nd ed. Reading, MA: W. A. Benjamin/Addison-Wesley, pp. 50-53, 1970.
Patterson, S. J. An Introduction to the Theory of the Riemann Zeta-Function. New York: Cambridge University Press, 1988.
Pegg, E. Jr. and Weisstein, E. W. "Seven Mathematical Tidbits." MathWorld Headline News. Nov. 8, 2004. ../topics/news/2004-11-08/seventidbits/#3.
Plouffe, S. "Identities Inspired from Ramanujan Notebooks." http://www.lacim.uqam.ca/~plouffe/identities.html.
Riemann, G. F. B. "Über die Anzahl der Primzahlen unter einer gegebenen Grösse." Monatsber. Königl. Preuss. Akad. Wiss. Berlin, 671-680, Nov. 1859.
Reprinted in Das Kontinuum und Andere Monographen (Ed. H. Weyl). New York: Chelsea, 1972.
Rivoal, T. "La fonction Zeta de Riemann prend une infinité de valeurs irrationnelles aux entiers impairs." Comptes Rendus Acad. Sci. Paris 331, 267-270, 2000.
Rivoal, T. "Irrationalité d'au moins un des neuf nombres ![]() ,
,![]() ,
,![]() .
.
Sloane, N. J. A. Sequences A001067, A002432/M4283, A006953/M2039, A057866, A057867, A076813, A093720, and A093721 in "The On-Line Encyclopedia of Integer Sequences." http://www.research.att.com/~njas/sequences/.
Sondow, J. "Analytic Continuation of Riemann's Zeta Function and Values at Negative Integers via Euler's Transformation of Series." Proc. Amer. Math. Soc. 120, 421-424, 1994.
Spanier, J. and Oldham, K. B. "The Zeta Numbers and Related Functions." Ch. 3 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 25-33, 1987.
Srivastava, H. M. "Some Simple Algorithms for the Evaluations and Representations of the Riemann Zeta Function at Positive Integer Arguments." J. Math. Anal. Appl. 246, 331-351, 2000.
Stieltjes, T. J. Oeuvres Complètes, Vol. 2 (Ed. G. van Dijk.) New York: Springer-Verlag, p. 100, 1993.
Titchmarsh, E. C. The Zeta-Function of Riemann. London: Cambridge University Press, 1930.
Titchmarsh, E. C. The Theory of the Riemann Zeta Function, 2nd ed. New York: Clarendon Press, 1987.
Tyler, D. and Chernhoff, P. "Problem 3103. An Odd Sum Reappears." Amer. Math. Monthly 92, 507, 1985.
Vardi, I. "The Riemann Zeta Function." Ch. 8 in Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 141-174, 1991.
Wagon, S. "The Riemann Zeta Function." §10.6 in Mathematica in Action. New York: W. H. Freeman, pp. 353-362, 1991.
Watkins,M. R. "Inexplicable Secrets of Creation." http://www.maths.ex.ac.uk/~mwatkins/zeta/.
![]() Weisstein, E. W. "Books about Riemann Zeta Function." http://www.ericweisstein.com/encyclopedias/books/RiemannZetaFunction.html.
Weisstein, E. W. "Books about Riemann Zeta Function." http://www.ericweisstein.com/encyclopedias/books/RiemannZetaFunction.html.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.
Woon, S. C. "Generalization of a Relation Between the Riemann Zeta Function and Bernoulli Numbers." 24 Dec 1998. http://arxiv.org/abs/math.NT/9812143/.
Zucker, I. J. "The Summation of Series of Hyperbolic Functions." SIAM J. Math. Anal. 10, 192-206, 1979.
Zucker, I. J. "Some Infinite Series of Exponential and Hyperbolic Functions." SIAM J. Math. Anal. 15, 406-413, 1984.
Zudilin, W. "One of the Numbers ![]() ,
,![]() ,
,![]() ,
,![]() Is Irrational." Uspekhi Mat. Nauk 56, 149-150, 2001.
Is Irrational." Uspekhi Mat. Nauk 56, 149-150, 2001.
Zvengrowski, P. and Saidak, F. "On the Modulus of the Riemann Zeta Function in the Critical Strip." Math. Slovaca 53, 145-172, 2003.
![]()