De complexe getallen is het lichaam ![]() van de getallen van de vorm
van de getallen van de vorm ![]() ,
,![]() .
.![]() wordt gebruikt als indicatie van een complex getal, nemeod men dit een "affix." In de cartesiaanse notatie, wordt
wordt gebruikt als indicatie van een complex getal, nemeod men dit een "affix." In de cartesiaanse notatie, wordt ![]() geschreven als. Het lichaam van de complexe getallen bevat het lichaam van de reele getallen als een sublichaam.
geschreven als. Het lichaam van de complexe getallen bevat het lichaam van de reele getallen als een sublichaam.
Doormiddel van de Euler formule, kan een complex getal
| (1) |
geschreven worden in de"polaire" notatie
| (2) |
Hier, is ![]() gekend als de complexe module en
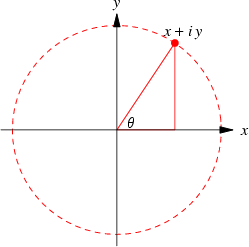
gekend als de complexe module en ![]() als het complexe argument of phase. De bovenstaande tekening toont wat gekend is als een Argand diagram van het punt z, waar de stippellijn cirkel de complex modulus
als het complexe argument of phase. De bovenstaande tekening toont wat gekend is als een Argand diagram van het punt z, waar de stippellijn cirkel de complex modulus ![]() voorstelt van z en waar de hoek
voorstelt van z en waar de hoek ![]() het complex argument voorstelt. Historisch gezien,is de geometrische voorstelling van een complex getal als een simpel punt in een vlak belangrijk omdat zo het idee van een complex getal meer acceptable was. In particular, "imaginary" numbers became accepted partly through their visualization.
het complex argument voorstelt. Historisch gezien,is de geometrische voorstelling van een complex getal als een simpel punt in een vlak belangrijk omdat zo het idee van een complex getal meer acceptable was. In particular, "imaginary" numbers became accepted partly through their visualization.
Unlike real numbers, complex numbers do not have a natural ordering, so there is no analog of complex-valued inequalities. This property is not so surprising however when the are viewed as being elements in the complex plane, since points in a plane also lack a natural ordering.
The absolute square of z is defined by ![]() ,
,![]() the complex conjugate, and the argument may be computed from
the complex conjugate, and the argument may be computed from
| (3) |
The real ![]() and imaginary parts
and imaginary parts ![]() are given by
are given by
| (4) | |||
| (5) |
de Moivre's identity relates powers of complex numbers for real n by
| (6) |
A power of complex number z to a positive integer exponent n can be written in closed form as
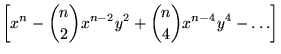 |
|||
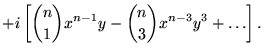 |
(7) |
The first few are explicitly
| (8) | |||
| (9) | |||
| (10) | |||
| (11) |
(Abramowitz and Stegun 1972).
| (12) |
| (13) |
| (14) |
and complex division
| (15) |
can also be defined for complex numbers. Complex numbers may also be taken to complex powers. For example, complex exponentiation obeys
| (16) |
where ![]() is the complex argument.
is the complex argument.
![]()
Absolute Square, Argand Diagram, Complex Argument, Complex Deling, Complex Machten, Complex Modulus, Complex Vermenigvuldiging, Complex Vlak, Complex Subtraction, i, Imaginair Getal, Phase, Phasor, Reele Getal, Surreal Getal
![]()
![]()
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 16-17, 1972.
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 353-357, 1985.
Bold, B. "Complex Numbers." Ch. 3 in Famous Problems of Geometry and How to Solve Them. New York: Dover, pp. 19-27, 1982.
Courant, R. and Robbins, H. "Complex Numbers." §2.5 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 88-103, 1996.
Ebbinghaus, H. D.; Hirzebruch, F.; Hermes, H.; Prestel, A; Koecher, M.; Mainzer, M.; and Remmert, R. Numbers. New York: Springer-Verlag, 1990.
Krantz, S. G. "Complex Arithmetic." §1.1 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 1-7, 1999.
Mazur, B. Imagining Numbers (Particularly the Square Root of Minus Fifteen). Farrar, Straus and Giroux, 2003.
Morse, P. M. and Feshbach, H. "Complex Numbers and Variables." §4.1 in Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 349-356, 1953.
Nahin, P. J. An Imaginary Tale: The Story of ![]() .
.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Complex Arithmetic." §5.4 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 171-172, 1992.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, pp. 21-23, 1986.
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 1168, 2002.