Een irrationeel getal is een getal niet kan uitgedrukt worden door een breuk ![]() waarbij p en q integers zijn. Irrationele getallen hebben een decimale uitbreiding die niet eindig is of periodiek . Elk transcendenteel getal is irrationeel.
waarbij p en q integers zijn. Irrationele getallen hebben een decimale uitbreiding die niet eindig is of periodiek . Elk transcendenteel getal is irrationeel.
Het meest bekende irrationeel getal is ![]() ,
,![]() de filosoofHippasus
de filosoofHippasus ![]() een geometrische methode gebruikte om de irrationale eigenschap van
een geometrische methode gebruikte om de irrationale eigenschap van![]() aan te tonen en dit op zee , zodat zijn vrienden ,fanatieke leerlingen van Pythagoras
aan te tonen en dit op zee , zodat zijn vrienden ,fanatieke leerlingen van Pythagoras ![]() , hem bij deze belangrijke ontdekking overboord smeten
, hem bij deze belangrijke ontdekking overboord smeten![]() ,
,![]() ,
,
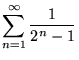 |
(1) | ||
| (2) |
(Erdos 1947) en een verzameling van veralgemening hiervan (Borwein 1992) zijn ook gekend als irrationeel (Bailey en Crandall 2001).
Getallen van de vorm ![]() zijn irrationeel tenzij n de mde macht is van een integer. Getallen van de vorm
zijn irrationeel tenzij n de mde macht is van een integer. Getallen van de vorm ![]() ,
,![]() het logaritme is, zijn irrationeel als m en n e integers zijn, een van beide heeft een priem factor waarbij de andere geen.
het logaritme is, zijn irrationeel als m en n e integers zijn, een van beide heeft een priem factor waarbij de andere geen. ![]() is irrationeel voor rationele getallen
is irrationeel voor rationele getallen ![]() .
.![]() is irrationeel voor elke niet-negatief rationeel getalr (Niven 1956, Stevens 1999), en
is irrationeel voor elke niet-negatief rationeel getalr (Niven 1956, Stevens 1999), en ![]() (waarbij
(waarbij ![]() gemeten wordt in graden ) is irrationeel voor elk rationeelgetal
gemeten wordt in graden ) is irrationeel voor elk rationeelgetal ![]() met de uitzondering voor
met de uitzondering voor ![]() (Niven 1956).
(Niven 1956). ![]() is irrationeel voor elk rattioneel getal
is irrationeel voor elk rattioneel getal ![]() (Stevens 1999).
(Stevens 1999).
De irrationaliteit van e is bewezen door by Euler ![]() in 1737.
in 1737.![]() is irrational voor positieve integrale getallen n. De irrationaliteit van
is irrational voor positieve integrale getallen n. De irrationaliteit van![]() is bewezen door Lambert
is bewezen door Lambert ![]() in 1760. Apéry's constant
in 1760. Apéry's constant ![]() (waarby
(waarby![]() deRiemann zeta function is ) is bewezen irrationeel te zijn by Apéry (Apéry 1979, van der Poorten 1979). als toeveogen heeft T. Rivoal (2000) recent bewezen dat er oneindig aantel integers n zodat
deRiemann zeta function is ) is bewezen irrationeel te zijn by Apéry (Apéry 1979, van der Poorten 1979). als toeveogen heeft T. Rivoal (2000) recent bewezen dat er oneindig aantel integers n zodat ![]() irrationeel zijn . Als bijlage heeft hij aangetoond minstens een van
irrationeel zijn . Als bijlage heeft hij aangetoond minstens een van ![]() ,
,![]() ,
,![]() irrationeel zijn (Rivoal 2001).
irrationeel zijn (Rivoal 2001).
Vanuit Gelfond's theorem, een getal met de vorm ![]() is transcendenteel (en daarom ook irrationeel) als a algebraisch bij
is transcendenteel (en daarom ook irrationeel) als a algebraisch bij ![]() ,
,![]() (daar
(daar![]() ),
), ![]() ,
,![]() .
.![]() irrationeel is. In feite, hij bewees dat
irrationeel is. In feite, hij bewees dat![]() ,
,![]() en
en![]() algebraisch onafhangkelijk zijn, maar er was nog niet gesteld dat
algebraisch onafhangkelijk zijn, maar er was nog niet gesteld dat ![]() irrationeel zijn.
irrationeel zijn.
Gegeven de polynomische vergelijking
| (3) |
waarbij![]() integers zijn , dan zijn de wortels
integers zijn , dan zijn de wortels![]() ofwel integralen of irrationeel.
ofwel integralen of irrationeel.
Als![]() irrationeel is , dan is dit ook zo voor
irrationeel is , dan is dit ook zo voor ![]() ,
,![]() ,
,![]() .
.
De Irrationaliteit is nog niet vastgesteld voor ![]() ,
,![]() ,
,![]() ,
,![]() (waar
(waar ![]() de Euler-Mascheroni constant is).
de Euler-Mascheroni constant is).
Hurwitz's irrationeel getal theorie geeft een bounds van de vorm
| (4) |
voor het best benaderde breuk for een willkeurig irrationeel getal![]() ,
,![]() de Lagrange getallen zijn en steeds groter is voor elk 'slechte ' paar van irrationele getallen dwelke zijn uitgesloten.
de Lagrange getallen zijn en steeds groter is voor elk 'slechte ' paar van irrationele getallen dwelke zijn uitgesloten.
De serieën
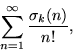 |
(5) |
waae ![]() de divisor function is, is irrationeel voor k = 1 en 2, en de serieën
de divisor function is, is irrationeel voor k = 1 en 2, en de serieën
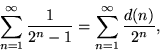 |
(6) |
waar d(n) het getal is van de breuk van n, zijn ook irrationeel (Guy 1994).
![]()
Algebraisch Integer, Algebraisch Getal, Bijna Integer, Decimale Uitbreiding, Dirichlet Function, e, Ferguson-Forcade Algorithm, Gelfond's Theorie, Hurwitz's Irrationeel Getal Theorie, Bijna Nobel Getal, Nobel Getal, Pi, Pythagoras's Constante, Pythagoras's Theorie, Regulier getal, Repeterend Decimaal, q-Harmonic Serie, Quadratic Irrationeel Getal, Rationeel Getal, Segre's Theorie, Transcendenteel Getal
![]()
![]()
Apéry, R. "Irrationalité de ![]() et
et ![]() .
.
Bailey, D. H. and Crandall, R. E. "Random Generators and Normal Numbers." To appear in Exper. Math. Preprint dated Feb. 22, 2003 available at http://www.nersc.gov/~dhbailey/dhbpapers/bcnormal.pdf.
Borwein, P. "On the Irrationality of Certain Series." Math. Proc. Cambridge Philos. Soc. 112, 141-146, 1992.
Courant, R. and Robbins, H. "Incommensurable Segments, Irrational Numbers, and the Concept of Limit." §2.2 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 58-61, 1996.
Erdos, P. "On Arithmetical Properties of Lambert Series." J. Indian Math. Soc. 12, 63-66, 1948.
Guy, R. K. "Some Irrational Series." §B14 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, p. 69, 1994.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.
Manning, H. P. Irrational Numbers and Their Representation by Sequences and Series. New York: Wiley, 1906.
Nagell, T. "Irrational Numbers" and "Irrationality of the numbers e and ![]() .
.
Nesterenko, Yu. "Modular Functions and Transcendence Problems." C. R. Acad. Sci. Paris Sér. I Math. 322, 909-914, 1996.
Nesterenko, Yu. V. "Modular Functions and Transcendence Questions." Mat. Sb. 187, 65-96, 1996.
Niven, I. M. Irrational Numbers. New York: Wiley, 1956.
Niven, I. M. Numbers: Rational and Irrational. New York: Random House, 1961.
Pappas, T. "Irrational Numbers & the Pythagoras Theorem." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 98-99, 1989.
Rivoal, T. "La fonction Zeta de Riemann prend une infinité de valeurs irrationnelles aux entiers impairs." Comptes Rendus Acad. Sci. Paris 331, 267-270, 2000.
Rivoal, T. "Irrationalité d'au moins un des neuf nombres ![]() ,
,![]() ,
,![]() .
.
Stevens, J. "Zur Irrationalität von ![]() .
.
van der Poorten, A. "A Proof that Euler Missed... Apéry's Proof of the Irrationality of ![]() .
.
![]() Weisstein, E. W. "Books about Irrational Numbers." http://www.ericweisstein.com/encyclopedias/books/IrrationalNumbers.html.
Weisstein, E. W. "Books about Irrational Numbers." http://www.ericweisstein.com/encyclopedias/books/IrrationalNumbers.html.