The roots (sometimes also called "zeros") of an equation

are the values of x for which the equation is satisfied.

Rolle proved that any complex number has n nth roots (Boyer 1968, p. 476). The nth root of a complex number z can be found in Mathematica as z^(1/n). The nth roots z of a complex number w can be found analytically by solving the equation

Then

so that the roots have complex modulus

and complex argument

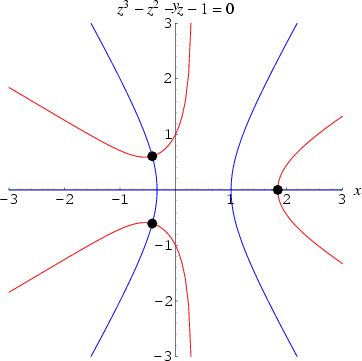
The roots of a complex function can be obtained by separating it into its real and imaginary plots and plotting these curves (which are related by the Cauchy-Riemann equations) separately. Their intersections give the complex roots of the original function. For example, the plot above shows the curves representing the real and imaginary parts of , with the three roots indicated as black points.

Householder (1970) gives an algorithm for constructing root-finding algorithms with an arbitrary order of convergence. Special root-finding techniques can often be applied when the function in question is a polynomial.

The fundamental theorem of algebra states that every polynomial equation of degree n has exactly n complex roots, where some roots may have a multiplicity greater than 1 (in which case they are said to be degenerate). In Mathematica, the expression Root[p(x), k] represents the kth root of the polynomial , where k = 1, ..., n is an index indicating the root number in Mathematica's ordering.

Root-Finding Algorithm, Descartes' Sign Rule, Fundamental Theorem of Symmetric Functions, Inside-Outside Theorem, Isograph, Multiplicity, Polynomial, Polynomial Roots, Root Dragging Theorem, Root Extraction, Root Separation, Rouché's Theorem, Simple Root, Sturm Function, Sturm Theorem, Vanishing, Weierstrass Approximation Theorem, Zero Set