Number Theory > Automorphic Forms > Modular Forms v

Modular Function

 

A function is said to be modular (or "elliptic modular") if it satisfies:

1. f is meromorphic in the upper half-plane H,
2. 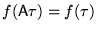for every matrix 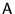in the modular group gamma,
3. The Laurent series of f has the form

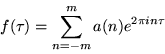
(Apostol 1997, p. 34). Every rational function of Klein's absolute invariant J is a modular function, and every modular function can be expressed as a rational function of J (Apostol 1997, p. 40). Modular functions are special cases of modular forms, but not vice versa.

An important property of modular functions is that if f is modular and not identically 0, then the number of zeros of f is equal to the number of poles of f in the closure of the fundamental region (Apostol 1997, p. 34).

 

Dirichlet Series, Elliptic Function, Elliptic Lambda Function, Elliptic Modular Function, Klein's Absolute Invariant, Modular Equation, Modular Form, Modular Group Gamma, Modular Group Gamma0, Modular Group Lambda




References

Apostol, T. M. Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, 1997.

Askey, R. In Ramanujan International Symposium (Ed. N. K Thakare). pp. 1-83.

Borwein, J. M. and Borwein, P. B. "Elliptic Modular Functions." §4.3 in Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, pp. 112-116, 1987.

Rademacher, H. "Zur Theorie der Modulfunktionen." J. reine angew. Math. 167, 312-336, 1932.

Rankin, R. A. Modular Forms and Functions. Cambridge, England: Cambridge University Press, 1977.

Schoeneberg, B. Elliptic Modular Functions: An Introduction. Berlin: New York: Springer-Verlag, 1974.

Weisstein, E. W. "Books about Modular Functions." http://www.ericweisstein.com/encyclopedias/books/ModularFunctions.html.