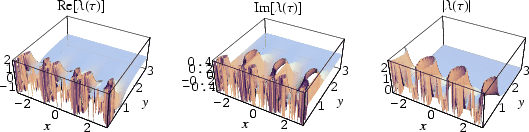
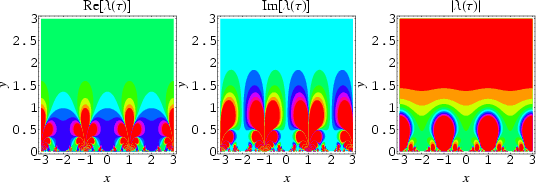
The elliptic lambda function ![]() is a
is a ![]() -modular function defined on the upper half-plane by
-modular function defined on the upper half-plane by
| (1) |
where ![]() is the half-period ratio, q is the nome
is the half-period ratio, q is the nome
| (2) |
and ![]() are theta functions.
are theta functions.
It is implemented as the Mathematica command ModularLambda[tau].
The elliptic lambda function ![]() satisfies the functional equations
satisfies the functional equations
| (3) | |||
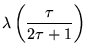 |
(4) |
![]() has the series expansion
has the series expansion
| (5) |
(Sloane's A014972), and ![]() has the series expansion
has the series expansion
| (6) |
(Sloane's A029845; Conway and Norton 1979; Borwein and Borwein 1987, p. 117).
![]() gives the value of the elliptic modulus
gives the value of the elliptic modulus ![]() for which the complementary
for which the complementary ![]() and normal complete elliptic integrals of the first kind K(k) are related by
and normal complete elliptic integrals of the first kind K(k) are related by
| (7) |
i.e., the elliptic integral singular value for r. It can be computed from
| (8) |
where
| (9) |
and ![]() is a Jacobi theta function.
is a Jacobi theta function. ![]() is related to
is related to ![]() by
by
| (10) |
For all rational r, ![]() and
and ![]() are known as elliptic integral singular values, and can be expressed in terms of a finite number of gamma functions (Selberg and Chowla 1967). Values of
are known as elliptic integral singular values, and can be expressed in terms of a finite number of gamma functions (Selberg and Chowla 1967). Values of ![]() for small r include
for small r include
| (11) | |||
| (12) | |||
| (13) | |||
| (14) | |||
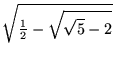 |
(15) | ||
| (16) | |||
| (17) | |||
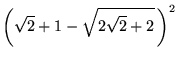 |
(18) | ||
| (19) | |||
| (20) | |||
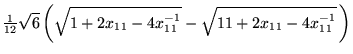 |
(21) | ||
| (22) | |||
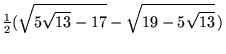 |
(23) | ||
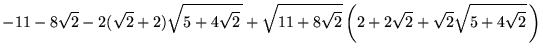 |
(24) | ||
| (25) | |||
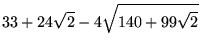 |
(26) | ||
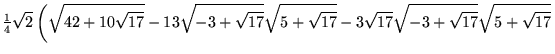 |
|||
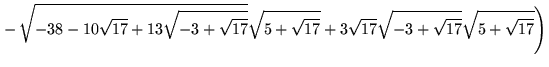 |
(27) | ||
| (28) |
where
| (29) |
The algebraic orders of these are given by 2, 2, 4, 2, 8, 4, 4, 4, 8, 4, 12, 4, 8, 8, 8, 4, ... (Sloane's A084540). ![]() is the first "hard" value, with an algebraic order apparently larger than 32.
is the first "hard" value, with an algebraic order apparently larger than 32.
Sone additional exact values are given by
| (30) | |||
| (31) | |||
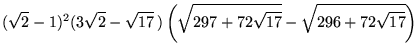 |
(32) | ||
| (33) | |||
| (34) | |||
| (35) |
Exact values can also be found for rational r, including
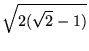 |
(36) | ||
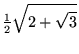 |
(37) | ||
| (38) | |||
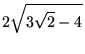 |
(39) | ||
| (40) | |||
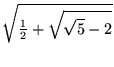 |
(41) | ||
| (42) | |||
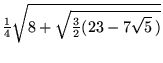 |
(43) | ||
| (44) | |||
| (45) |
where
![]() is related to the Ramanujan g- and G-functions by
is related to the Ramanujan g- and G-functions by
| (46) | |||
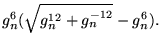 |
(47) |
![]()
Dedekind Eta Function, Elliptic Alpha Function, Elliptic Integral of the First Kind, Elliptic Modulus, Elliptic Integral Singular Value, j-Function, Jacobi Theta Functions, Klein's Absolute Invariant, Modular Function, Modular Group Lambda, Ramanujan g- and G-Functions
![]()
![]()
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, pp. 139 and 298, 1987.
Bowman, F. Introduction to Elliptic Functions, with Applications. New York: Dover, pp. 75, 95, and 98, 1961.
Conway, J. H. and Norton, S. P. "Monstrous Moonshine." Bull. London Math. Soc. 11, 308-339, 1979.
Selberg, A. and Chowla, S. "On Epstein's Zeta-Function." J. reine angew. Math. 227, 86-110, 1967.
Sloane, N. J. A. Sequences A014972, A029845, and A084540 in "The On-Line Encyclopedia of Integer Sequences." http://www.research.att.com/~njas/sequences/.
Watson, G. N. "Some Singular Moduli (1)." Quart. J. Math. 3, 81-98, 1932.
![]()