Ramanujan g- and G-Functions

Following Ramanujan (1913-14), write

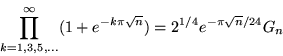(1)

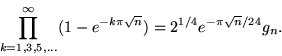(2)

These satisfy the equalities

			(3)
			(4)
			(5)
			(6)

and

can be derived using the theory of modular functions and can always be expressed as roots of algebraic equations when n is rational. For simplicity, Ramanujan tabulated

for n even and

for n odd. However, (6) allows

and

to be solved for in terms of

and

, giving

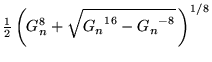			(7)
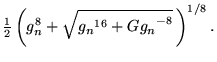			(8)

Using (3) and the above two equations allows

to be computed in terms of

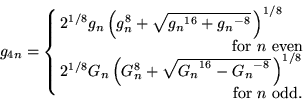(9)

In terms of the parameter k and complementary parameter ,

			(10)
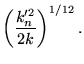			(11)

Here,

(12)

is the elliptic lambda function, which gives the value of k for which

(13)

Solving for gives

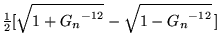			(14)
			(15)

Analytic values for small values of n can be found in Ramanujan

(1913-1914) and Borwein and Borwein (1987), and have been compiled by Weisstein. Ramanujan

(1913-1914) contains a typographical error labeling

Barnes G-Function

Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, pp. 139 and 298, 1987.

Ramanujan, S. "Modular Equations and Approximations to ." Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.