
Let ![]() and
and ![]() be periods of a doubly periodic function, with
be periods of a doubly periodic function, with ![]() the half-period ratio a number with
the half-period ratio a number with ![]() .
.
| (1) |
where ![]() and
and ![]() are the invariants of the Weierstrass elliptic function with modular discriminant
are the invariants of the Weierstrass elliptic function with modular discriminant
| (2) |
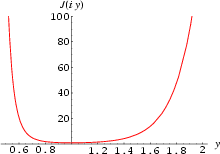
(Klein 1877). If ![]() ,
,
| (3) |
is a function of the ratio ![]() only, as are
only, as are ![]() ,
,![]() ,
,![]() .
.![]() ,
,![]() ,
,![]() ,
,![]() are analytic in H (Apostol 1997, p. 15).
are analytic in H (Apostol 1997, p. 15).
Klein's absolute invariant is implemented in Mathematica as KleinInvariantJ[tau].
The function ![]() is the same as the j-function, modulo a constant multiplicative factor.
is the same as the j-function, modulo a constant multiplicative factor.
Every rational function of J is a modular function, and every modular function can be expressed as a rational function of J (Apostol 1997, p. 40).
Klein's invariant can be given explicitly by
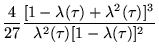 |
(4) | ||
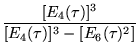 |
(5) |
(Klein 1878/79, Cohn 1994), where
| (6) |
![]() is a Jacobi theta function, the
is a Jacobi theta function, the ![]() are Ramanujan-Eisenstein series, and q is the nome. Klein's invariant can also be simply expressed in terms of the five Weber functions
are Ramanujan-Eisenstein series, and q is the nome. Klein's invariant can also be simply expressed in terms of the five Weber functions ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() is invariant under a unimodular transformation, so
is invariant under a unimodular transformation, so
| (7) |
and ![]() is a modular function.
is a modular function. ![]() takes on the special values
takes on the special values
| (8) | |||
| (9) | |||
| (10) |
![]() satisfies the functional equations
satisfies the functional equations
| (11) | |||
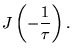 |
(12) |
It satisfies a number of beautiful multiple-argument identities, including the duplication formula
| (13) | |||
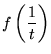 |
(14) |
with
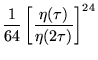 |
(15) | ||
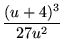 |
(16) |
and
| (17) | |||
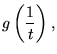 |
(18) |
with
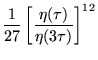 |
(19) | ||
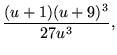 |
(20) |
and the quintuplication formula
| (21) | |||
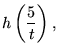 |
(22) |
with
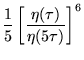 |
(23) | ||
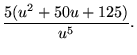 |
(24) |
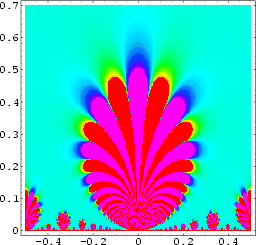
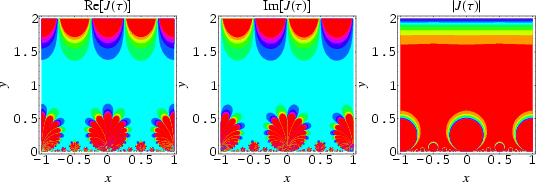
Plotting the real or imaginary part of ![]() in the complex plane produces a beautiful fractal-like structure illustrated above.
in the complex plane produces a beautiful fractal-like structure illustrated above.
![]()
Elliptic Lambda Function, j-Function, Jacobi Theta Functions, Pi, Ramanujan-Eisenstein Series, Weber Functions
![]()
![]()
Apostol, T. M. "Klein's Modular Function ![]() ,
,![]() and
and ![]() ,
,
Brezhnev, Y. V. "Uniformisation: On the Burnside Curve ![]() .
.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, pp. 115 and 179, 1987.
Cohn, H. Introduction to the Construction of Class Fields. New York: Dover, p. 73, 1994.
Klein, F. "Sull' equazioni dell' Icosaedro nella risoluzione delle equazioni del quinto grado [per funzioni ellittiche]." Reale Istituto Lombardo, Rendiconto, Ser. 2 10, 1877.
Klein, F. "Über die Transformation der elliptischen Funktionen und die Auflösung der Gleichungen fünften Grades." Math. Ann. 14, 1878/79.
Nesterenko, Yu. V. A Course on Algebraic Independence: Lectures at IHP 1999. http://www.math.jussieu.fr/~nesteren/.
![]()