The modular equation of degree n gives an algebraic connection of the form
| (1) |
between the transcendental complete elliptic integrals of the first kind with moduli k and l. When k and l satisfy a modular equation, a relationship of the form
| (2) |
exists, and M is called the multiplier. In general, if p is an odd prime, then the modular equation is given by
| (3) |
where
| (4) |
![]() is a elliptic lambda function, and
is a elliptic lambda function, and
| (5) |
(Borwein and Borwein 1987, p. 126). An elliptic integral identity gives
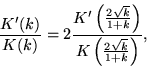 |
(6) |
so the modular equation of degree 2 is
| (7) |
which can be written as
| (8) |
A few low order modular equations written in terms of k and l are
| |
(9) |
| |
(10) |
| |
|
| (11) |
| (12) | |||
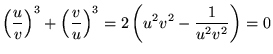 |
|||
| (13) | |||
| (14) |
where
| (15) |
and
| (16) |
Here, ![]() are Jacobi theta functions.
are Jacobi theta functions.
A modular equation of degree ![]() for
for ![]() can be obtained by iterating the equation for
can be obtained by iterating the equation for ![]() .
.
Quadratic modular identities include
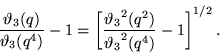 |
(17) |
Cubic identities include
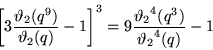 |
(18) |
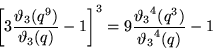 |
(19) |
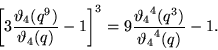 |
(20) |
A seventh-order identity is
| (21) |
From Ramanujan (1913-1914),
| (22) |
| (23) |
When k and l satisfy a modular equation, a relationship of the form
| (24) |
exists, and M is called the multiplier. The multiplier of degree n can be given by
| (25) |
where ![]() is a Jacobi theta function and K(k) is a complete elliptic integral of the first kind.
is a Jacobi theta function and K(k) is a complete elliptic integral of the first kind.
The first few multipliers in terms of l and k are
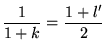 |
(26) | ||
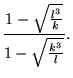 |
(27) |
In terms of the u and v defined for modular equations,
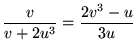 |
(28) | ||
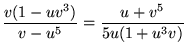 |
(29) | ||
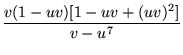 |
|||
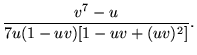 |
(30) |
![]()
Modular Form, Modular Function, Schläfli's Modular Form
![]()
![]()
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, pp. 127-132, 1987.
Hanna, M. "The Modular Equations." Proc. London Math. Soc. 28, 46-52, 1928.
Ramanujan, S. "Modular Equations and Approximations to ![]() .
.
![]()