Let G be a subgroup of the modular group gamma. Then an open subset of the upper half-plane H is called a fundamental region of G if

1. No two distinct points of 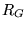are equivalent under G,

2. If 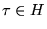, 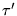then there is a point in the closure of 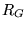such that 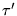is equivalent to 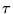under G.

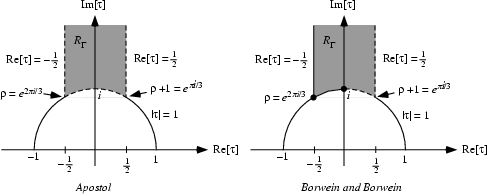
A fundamental region of the modular group gamma is given by such that and , illustrated above, where is the complex conjugate of (Apostol 1997, p. 31). Borwein and Borwein (1987, p. 113) define the boundaries of the region slightly differently by including the boundary points with .

 

Modular Group Gamma, Modular Group Lambda, Upper Half-Plane, Valence