The gamma group ![]() is the set of all transformations w of the form
is the set of all transformations w of the form
where a, b, c, and d are integers and ![]() .
.
A ![]() -modular function is then defined (Borwein and Borwein 1987, p. 114) as a function f that satisfies:
-modular function is then defined (Borwein and Borwein 1987, p. 114) as a function f that satisfies:
- 1. f is meromorphic in the upper half-plane
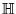 .
. - 2.
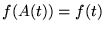 for all
for all 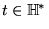 ,
,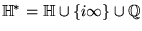 .
. - 3. f(t) tends to a limit (possibly infinite in the sense that
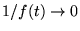 ) as t tends to the vertices of the fundamental region
) as t tends to the vertices of the fundamental region 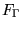 where the approach is from within the fundamental region
where the approach is from within the fundamental region 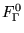 .
.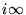 ,
,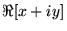 as
as 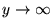 .
.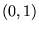 ,
,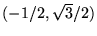 and
and 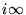 .
.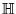 ,
,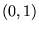 and
and 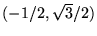 and need be checked only at
and need be checked only at 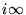 .
.
acobi Theta Functions, Klein's Absolute Invariant, Lambda Group
![]()
![]()
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, 1987.
![]()