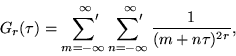Eisenstein Series

(1)

where the sum excludes , , and r is an integer with r > 2. The Eisenstein series satisfies the remarkable property

(2)

if the matrix 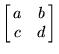is in the special linear group (Serre 1973, pp. 79 and 83). Therefore, is a modular form of weight (Serre 1973, p. 83).

Furthermore, each Eisenstein series is expressible as a polynomial of the elliptic invariants and of the Weierstrass elliptic function with positive rational coefficients (Apostol 1997).

The Eisenstein series of even order satisfy

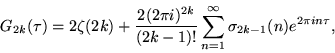(3)

where is the Riemann zeta function and is the divisor function (Apostol 1997, pp. 24 and 69). Writing the nome q as

(4)

where K(k) is a complete elliptic integral of the first kind, , k is the elliptic modulus, and defining

(5)

we have

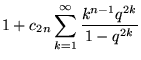			(6)
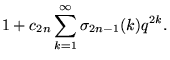			(7)

where

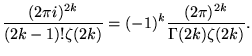			(8)
			(9)

where

is a Bernoulli number. For n = 1, 2, ..., the first few values of

are -24, 240, -504, 480, -264,

, ... (Sloane's A006863 and A001067).

The first few values of are therefore

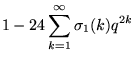			(10)
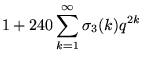			(11)
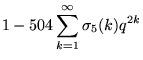			(12)
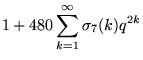			(13)
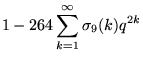			(14)
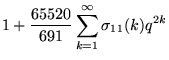			(15)
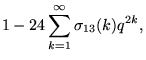			(16)

(Apostol 1997, p. 139). Ramanujan used the notations

, and

, and these functions satisfy the system of differential equations

			(17)
			(18)
			(19)

(Nesterenko 1999), where

is the differential operator.

can also be expressed in terms of complete elliptic integrals of the first kind K(k) as

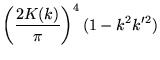			(20)
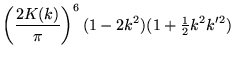			(21)

(Ramanujan 1913-1914), where k is the elliptic modulus.

The following table gives the first few Eisenstein series for even n.

n	Sloane	lattice
2	A006352
4	A004009
6	A013973
8	A008410
10	A013974

Ramanujan (1913-1914) used the notation L(q) to refer to the closely related function

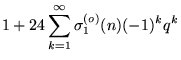			(22)

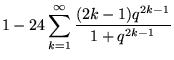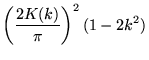			(23)
			(24)

(Sloane's A004011), where

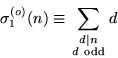(25)

is the odd divisor function. Ramanujan used the notation M(q) and N(q) to refer to and , respectively.

Divisor Function, Elliptic Invariants, Klein's Absolute Invariant, Leech Lattice, Pi, Theta Series, Weierstrass Elliptic Function

Apostol, T. M. "The Eisenstein Series and the Invariants and " and "The Eisenstein Series ." §1.9 and 3.10 in Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 12-13 and 69-71, 1997.

Borcherds, R. E. "Automorphic Forms on and Generalized Kac-Moody Algebras." In Proc. Internat. Congr. Math., Vol. 2. pp. 744-752, 1994.

Borwein, J. M. and Borwein, P. B. "Class Number Three Ramanujan Type Series for ." J. Comput. Appl. Math. 46, 281-290, 1993.

Bump, D. Automorphic Forms and Representations. Cambridge, England: Cambridge University Press, p. 29, 1997.

Conway, J. H. and Sloane, N. J. A. Sphere Packings, Lattices, and Groups, 2nd ed. New York: Springer-Verlag, pp. 119 and 123, 1993.

Coxeter, H. S. M. "Integral Cayley Numbers."The Beauty of Geometry: Twelve Essays. New York: Dover, pp. 20-39, 1999.

Gunning, R. C. Lectures on Modular Forms. Princeton, NJ: Princeton Univ. Press, p. 53, 1962.

Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, p. 166, 1999.

Milne, S. C. "Hankel Determinants of Eisenstein Series." 13 Sep 2000. http://arxiv.org/abs/math.NT/0009130/.

Nesterenko, Yu. V. §8.1 in A Course on Algebraic Independence: Lectures at IHP 1999. http://www.math.jussieu.fr/~nesteren/.

Ramanujan, S. "Modular Equations and Approximations to ." Quart. J. Pure Appl. Math. 45, 350-372, 1913-1914.

Serre, J.-P. A Course in Arithmetic. New York: Springer-Verlag, 1973.

Shimura, G. Euler Products and Eisenstein Series. Providence, RI: Amer. Math. Soc., 1997.

Sloane, N. J. A. Sequences A001067, A004009/M5416, A004011/M5140, A006863/M5150, A008410, A013973, and A013974 in "The On-Line Encyclopedia of Integer Sequences." http://www.research.att.com/~njas/sequences/.