A Dirichlet L-series is a series of the form
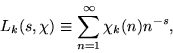 |
(1) |
where the number theoretic character ![]() is an integer function with period k, are called Dirichlet L-series. These series are very important in additive number theory (they were used, for instance, to prove Dirichlet's theorem), and have a close connection with modular forms. Dirichlet L-series can be written as sums of Lerch transcendents with z a power of
is an integer function with period k, are called Dirichlet L-series. These series are very important in additive number theory (they were used, for instance, to prove Dirichlet's theorem), and have a close connection with modular forms. Dirichlet L-series can be written as sums of Lerch transcendents with z a power of ![]() .
.
The generalized Riemann hypothesis conjectures that neither the Riemann zeta function nor any Dirichlet L-series has a zero with real part larger than 1/2.
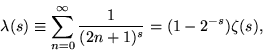 |
(2) |
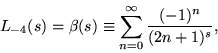 |
(3) |
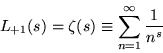 |
(4) |
are all Dirichlet L-series (Borwein and Borwein 1987, p. 289).
Hecke found a remarkable connection between each modular form with Fourier series
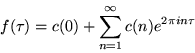 |
(5) |
and the Dirichlet L-series
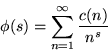 |
(6) |
This Dirichlet series converges absolutely for ![]() (if f is a cusp form) and
(if f is a cusp form) and ![]() if f is not a cusp form. In particular, if the coefficients c(n) satisfy the multiplicative property
if f is not a cusp form. In particular, if the coefficients c(n) satisfy the multiplicative property
| (7) |
then the Dirichlet L-series will have a representation of the form
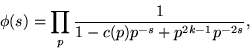 |
(8) |
which is absolutely convergent with the Dirichlet series (Apostol 1997, pp. 136-137). In addition, let ![]() be an even integer, then
be an even integer, then ![]() can be analytically continued beyond the line
can be analytically continued beyond the line ![]() such that
such that
- 1. If
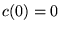 ,
,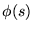 is an entire function of s,
is an entire function of s, - 2. If
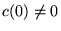 ,
,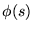 is analytic for all s except a single simple pole at s = k with complex residue
is analytic for all s except a single simple pole at s = k with complex residue
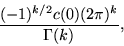
(9)
where
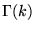 is the gamma function, and
is the gamma function, and - 3.
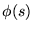 satisfies
satisfies
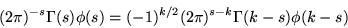
(10)
The number theoretic character ![]() is called primitive if the conductor
is called primitive if the conductor ![]() .
.![]() is imprimitive. A primitive L-series modulo k is then defined as one for which
is imprimitive. A primitive L-series modulo k is then defined as one for which ![]() is primitive. All imprimitive L-series can be expressed in terms of primitive L-series.
is primitive. All imprimitive L-series can be expressed in terms of primitive L-series.
Let P = 1 or ![]() ,
,![]() are distinct odd primes. Then there are three possible types of primitive L-series with real coefficients. The requirement of real coefficients restricts the number theoretic character to
are distinct odd primes. Then there are three possible types of primitive L-series with real coefficients. The requirement of real coefficients restricts the number theoretic character to ![]() for all k and n. The three type are then
for all k and n. The three type are then
- 1. If k = P (e.g., k = 1, 3, 5, ...) or
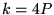 (e.g., k = 4, 12, 20, ...), there is exactly one primitive L-series.
(e.g., k = 4, 12, 20, ...), there is exactly one primitive L-series. - 2. If
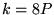 (e.g., k = 8, 24, ...), there are two primitive L-series.
(e.g., k = 8, 24, ...), there are two primitive L-series. - 3. If
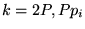 ,
,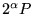 where
where 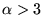 (e.g., k = 2, 6, 9, ...), there are no primitive L-series
(e.g., k = 2, 6, 9, ...), there are no primitive L-series
| (11) |
Primitive L-series of these types are denoted ![]() .
.
| (12) |
If ![]() ,
,
| (13) |
and if ![]() ,
,
The first few primitive negative L-series are ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
The Kronecker symbol ![]() is a real number theoretic character modulo d, and is in fact essentially the only type of real primitive number theoretic character mod d (Ayoub 1963). Therefore,
is a real number theoretic character modulo d, and is in fact essentially the only type of real primitive number theoretic character mod d (Ayoub 1963). Therefore,
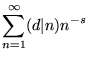 |
(14) | ||
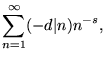 |
(15) |
where
Since the Kronecker symbols are periodic with period d, these equations can be written in the form of ![]() sums, each of which can be expressed in terms of the polygamma function
sums, each of which can be expressed in terms of the polygamma function ![]() ,
,
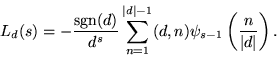 |
(16) |
Some specific values of primitive L-series are
| (17) | |||
| (18) | |||
| (19) | |||
| (20) | |||
| (21) | |||
| (22) | |||
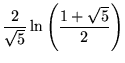 |
(23) | ||
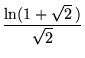 |
(24) | ||
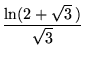 |
(25) | ||
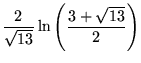 |
(26) | ||
| (27) | |||
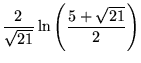 |
(28) | ||
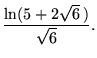 |
(29) |
The functional equations for ![]() are
are
| (30) | |||
| (31) |
For m a positive integer
| (32) | |||
| (33) | |||
| (34) | |||
| (35) | |||
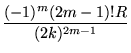 |
(36) | ||
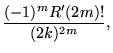 |
(37) |
where R and
![]() can be expressed in terms of transcendentals by
can be expressed in terms of transcendentals by
| (38) |
where h(d) is the class number and ![]() is the Dirichlet structure constant.
is the Dirichlet structure constant.
No general forms are known for ![]() and
and ![]() in terms of known transcendentals. Special examples include
in terms of known transcendentals. Special examples include
| (39) |
where K is defined as Catalan's constant, and
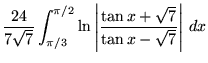 |
(40) | ||
| (41) | |||
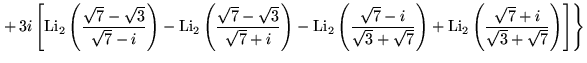 |
(42) | ||
| (43) |
(Sloane's A103133), where
![]()
Dirichlet Beta Function, Dirichlet Eta Function, Dirichlet Series, Double Sum, Generalized Riemann Hypothesis, Hecke L-Series, Modular Form, Petersson Conjecture
![]()
![]()
Apostol, T. M. Introduction to Analytic Number Theory. New York: Springer-Verlag, 1976.
Apostol, T. M. "Modular Forms and Dirichlet Series" and "Equivalence of Ordinary Dirichlet Series." §6.16 and §8.8 in Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 136-137 and 174-176, 1997.
Ayoub, R. G. An Introduction to the Analytic Theory of Numbers. Providence, RI: Amer. Math. Soc., 1963.
Bailey, D. H. and Borwein, J. M. "Experimental Mathematics: Examples, Methods, and Implications." Oct. 7, 2004, http://www.cs.dal.ca/~jborwein/ams-expmath.pdf.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, 1987.
Buell, D. A. "Small Class Numbers and Extreme Values of L-Functions of Quadratic Fields." Math. Comput. 139, 786-796, 1977.
Hecke, E. "Über die Bestimmung Dirichletscher Reihen durch ihre Funktionalgleichung." Math. Ann. 112, 664-699, 1936.
Ireland, K. and Rosen, M. "Dirichlet L-Functions." Ch. 16 in A Classical Introduction to Modern Number Theory, 2nd ed. New York: Springer-Verlag, pp. 249-268, 1990.
Koch, H. "L-Series." Ch. 7 in Number Theory: Algebraic Numbers and Functions. Providence, RI: Amer. Math. Soc., pp. 203-258, 2000.
Shanks, D. and Wrench, J. W. Jr. "The Calculation of Certain Dirichlet Series." Math. Comput. 17, 135-154, 1963.
Shanks, D. and Wrench, J. W. Jr. "Corrigendum to 'The Calculation of Certain Dirichlet Series."' Math. Comput. 17, 488, 1963.
Sloane, N. J. A. Sequences A003657/M2332, A003658/M3776, and A103133 in "The On-Line Encyclopedia of Integer Sequences." http://www.research.att.com/~njas/sequences/.
Zucker, I. J. and Robertson, M. M. "Some Properties of Dirichlet L-Series." J. Phys. A: Math. Gen. 9, 1207-1214, 1976.
![]()