Petersson considered the absolutely converging Dirichlet L-series
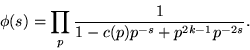
Writing the denominator as
where
and
Petersson conjectured that 
and 
are always complex conjugate, which implies
and
This conjecture was proven by Deligne (1974), which also proved the tau conjecture as a special case. Deligne was awarded the Fields medal for his proof.
Dirichlet L-Series, Tau Conjecture
Apostol, T. M. Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, p. 140, 1997.
Deligne, P. "La conjecture de Weil. I." Inst. Hautes Études Sci. Publ. Math. 43, 273-307, 1974.
Deligne, P. "La conjecture de Weil. II." Inst. Hautes Études Sci. Publ. Math. 52, 137-252, 1980.