A cusp form is a modular form for which the coefficient 
in the Fourier series
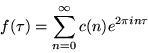
(Apostol 1997, p. 114). The only entire cusp form of weight k < 12 is the zero function (Apostol 1997, p. 116). The set of all cusp forms in 
(all modular forms of weight k) is a linear subspace of which is denoted 
. is 1 for k = 12, 16, 18, 20, 22, and 26 (Apostol 1997, p. 119). For a cusp form 
,
 |
(1) |
(Apostol 1997, p. 135) or, more precisely,
 |
(2) |
for every 
(Selberg 1965; Apostol 1997, p. 136). It is conjectured that the 
in the exponent can be reduced to 
(Apostol 1997, p. 136).
Apostol, T. M. Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 114 and 116, 1997.
Selberg, A. "On the Estimate of Coefficients of Modular Forms." Proc. Sympos. Pure Math. 8, 1-15, 1965.