
The totient function ![]() ,
,![]() that are relatively prime to (i.e., do not contain any factor in common with) n, where 1 is counted as being relatively prime to all numbers. Since a number less than or equal to and relatively prime to a given number is called a totative, the totient function
that are relatively prime to (i.e., do not contain any factor in common with) n, where 1 is counted as being relatively prime to all numbers. Since a number less than or equal to and relatively prime to a given number is called a totative, the totient function ![]() can be simply defined as the number of totatives of n. For example, there are eight totatives of 24 (1, 5, 7, 11, 13, 17, 19, and 23), so
can be simply defined as the number of totatives of n. For example, there are eight totatives of 24 (1, 5, 7, 11, 13, 17, 19, and 23), so ![]() .
.
![]() is always even for
is always even for ![]() .
.![]() ,
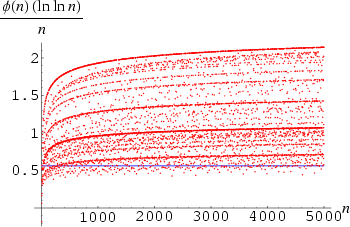
,![]() for n = 1, 2, ... are 1, 1, 2, 2, 4, 2, 6, 4, 6, 4, 10, ... (Sloane's A000010). The totient function is given by the Möbius transform of 1, 2, 3, 4, ... (Sloane and Plouffe 1995, p. 22).
for n = 1, 2, ... are 1, 1, 2, 2, 4, 2, 6, 4, 6, 4, 10, ... (Sloane's A000010). The totient function is given by the Möbius transform of 1, 2, 3, 4, ... (Sloane and Plouffe 1995, p. 22). ![]() is plotted above for small n.
is plotted above for small n.
For a prime p,
| (1) |
since all numbers less than p are relatively prime to p. If ![]() is a power of a prime, then the numbers that have a common factor with m are the multiples of p: p,
is a power of a prime, then the numbers that have a common factor with m are the multiples of p: p, ![]() ,
,![]() .
.![]() of these multiples, so the number of factors relatively prime to
of these multiples, so the number of factors relatively prime to ![]() is
is
| (2) |
Now take a general m divisible by p. Let ![]() be the number of positive integers
be the number of positive integers ![]() not divisible by p. As before, p,
not divisible by p. As before, p, ![]() ,
,![]() have common factors, so
have common factors, so
| (3) |
Now let q be some other prime dividing m. The integers divisible by q are q, ![]() ,
,![]() .
.![]() ,
,![]() .
.![]() to obtain
to obtain ![]() is
is
| (4) |
and
 |
|||
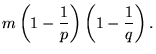 |
(5) |
By induction, the general case is then
| (6) |
An interesting identity relates ![]() to
to ![]() ,
,
| (7) |
Another identity relates the divisors d of n to n via
| (8) |
The totient function satisfies the inequality
| (9) |
for all n except n = 2 and n = 6 (Kendall and Osborn 1965; Mitrinovic and Sándor 1995, p. 9). Therefore, the only values of n for which ![]() are n = 3, 4, and 6. In addition, for composite n,
are n = 3, 4, and 6. In addition, for composite n,
| (10) |
(Sierpinski and Schinzel 1988; Mitrinovic and Sándor 1995, p. 9).
![]() also satisfies
also satisfies
| (11) |
where ![]() is the Euler-Mascheroni constant. The values of n for which
is the Euler-Mascheroni constant. The values of n for which ![]() are given by 3, 4, 5, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 22, ... (Sloane's A100966).
are given by 3, 4, 5, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 22, ... (Sloane's A100966).
The divisor function satisfies the congruence
| (12) | |||
 |
(13) |
for all primes
| (14) |
(Honsberger 1976, p. 35).
The first few n for which
| (15) |
are given by 1, 3, 15, 104, 164, 194, 255, 495, 584, 975, ... (Sloane's A001274), which have common values ![]() ,
,
The only ![]() for which
for which
| (16) |
is n = 5186, giving
| (17) |
(Guy 1994, p. 91).
Arithmetic progressions of n giving consecutive values include
| |
(18) |
| |
(19) |
(Guy 1994, p. 91). McCranie found an arithmetic progression of six numbers with equal totient functions,
| |
|
| |
(20) |
If the Goldbach conjecture is true, then for every positive integer m, there are primes p and q such that
| (21) |
(Guy 1994, p. 105). Erdos asked if this holds for p and q not necessarily prime, but this relaxed form remains unproven (Guy 2004, p. 160).
Guy (1994, p. 99) discussed solutions to
| (22) |
where ![]() is the divisor function. F. Helenius has found 365 such solutions, the first of which are 2, 8, 12, 128, 240, 720, 6912, 32768, 142560, 712800, ... (Sloane's A001229).
is the divisor function. F. Helenius has found 365 such solutions, the first of which are 2, 8, 12, 128, 240, 720, 6912, 32768, 142560, 712800, ... (Sloane's A001229).
![]()
Dedekind Function, Euler's Totient Rule, Fermat's Little Theorem, Lehmer's Totient Problem, Leudesdorf Theorem, Noncototient, Nontotient, Silverman Constant, Totative, Totient Summatory Function, Totient Valence Function
![]()
![]()
Abramowitz, M. and Stegun, I. A. (Eds.). "The Euler Totient Function." §24.3.2 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 826, 1972.
Beiler, A. H. Ch. 12 in Recreations in the Theory of Numbers: The Queen of Mathematics Entertains. New York: Dover, 1966.
Cohen, G. L. and Segal, S. L. "A Note Concerning Those n for which ![]() Divides n." Fib. Quart. 27, 285-286, 1989.
Divides n." Fib. Quart. 27, 285-286, 1989.
Conway, J. H. and Guy, R. K. "Euler's Totient Numbers." The Book of Numbers. New York: Springer-Verlag, pp. 154-156, 1996.
Courant, R. and Robbins, H. "Euler's ![]() Function. Fermat's Theorem Again." §2.4.3 in Supplement to Ch. 1 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 48-49, 1996.
Function. Fermat's Theorem Again." §2.4.3 in Supplement to Ch. 1 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 48-49, 1996.
Guy, R. K. "Euler's Totient Function," "Does ![]() Properly Divide
Properly Divide ![]() ,
,![]() ,
,![]() and
and ![]() ,
,![]() and
and ![]() .
.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 115-116, 2003.
Helenius, F. Untitled. http://pweb.netcom.com/~fredh/phisigma/pslist.html.
Honsberger, R. Mathematical Gems II. Washington, DC: Math. Assoc. Amer., p. 35, 1976.
Jones, G. A. and Jones, J. M. "Euler's Function." Ch. 5 in Elementary Number Theory. Berlin: Springer-Verlag, pp. 83-96, 1998.
Kendall, D. G. and Osborn, R. "Two Simple Lower Bounds for Euler's Function." Texas J. Sci. 17, 1965.
Mitrinovic, D. S. and Sándor, J. Handbook of Number Theory. Dordrecht, Netherlands: Kluwer, 1995.
Nagell, T. "Relatively Prime Numbers. Euler's ![]() -Function." §8 in Introduction to Number Theory. New York: Wiley, pp. 23-26, 1951.
-Function." §8 in Introduction to Number Theory. New York: Wiley, pp. 23-26, 1951.
Niven, I. M.; Zuckerman, H. S.; and Montgomery, H. L. An Introduction to the Theory of Numbers, 5th ed. New York: Wiley, p. 51, 1991.
Perrot, J. 1811. Quoted in Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Chelsea, p. 126, 1952.
Séroul, R. "The Euler Phi Function." §2.7 in Programming for Mathematicians. Berlin: Springer-Verlag, pp. 14-15, 2000.
Shanks, D. "Euler's ![]() Function." §2.27 in Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 68-71, 1993.
Function." §2.27 in Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 68-71, 1993.
Sierpinski, W. and Schinzel, A. Elementary Theory of Numbers, 2nd Eng. ed. Amsterdam, Netherlands: North-Holland, 1988.
Sloane, N. J. A. Sequences A000010/M0299, A001229, A001274/M2999, A002088/M1008, A003275/M1874, A050518, and A100966 in "The On-Line Encyclopedia of Integer Sequences." http://www.research.att.com/~njas/sequences/.
Sloane, N. J. A. and Plouffe, S. The Encyclopedia of Integer Sequences. San Diego, CA: Academic Press, 1995.
Subbarao, M. V. "On Two Congruences for Primality." Pacific J. Math. 52, 261-268, 1974.
![]()