Goldbach's original conjecture (sometimes called the "ternary" Goldbach conjecture), written in a June 7, 1742 letter to Euler, 
states "at least it seems that every number that is greater than 2 is the sum of three primes" (Goldbach 1742; Dickson 1957, p. 421). Note that here Goldbach considered the number 1 to be a prime, a convention that is no longer followed. As re-expressed by Euler, an equivalent form of this conjecture (called the "strong" or "binary" Goldbach conjecture) asserts that all positive even integers 
can be expressed as the sum of two primes. Two primes (p, q) such that 
for n a positive integer are sometimes called a Goldbach partition (Oliveira e Silva).
According to Hardy (1999, p. 19), "It is comparatively easy to make clever guesses; indeed there are theorems, like 'Goldbach's Theorem,' which have never been proved and which any fool could have guessed." Faber and Faber offered a 
prize to anyone who proved Goldbach's conjecture between March 20, 2000 and March 20, 2002, but the prize went unclaimed and the conjecture remains open.
Schnirelman (1939) proved that every even number can be written as the sum of not more than 
primes (Dunham 1990), which seems a rather far cry from a proof for two primes! Pogorzelski (1977) claimed to have proven the Goldbach conjecture, but his proof is not generally accepted (Shanks 1993). The following table summarizes bounds n such that the strong Goldbach conjecture has been shown to be true for numbers 
.
| bound | reference |
 |
Desboves 1885 |
 |
Pipping 1938 |
 |
Stein and Stein 1965ab |
 |
Granville et al. 1989 |
 |
Sinisalo 1993 |
 |
Deshouillers et al. 1998 |
 |
Richstein 2001 |
 |
Oliveira e Silva (Mar. 24, 2003) |
 |
Oliveira e Silva (Oct. 3, 2003) |
 |
Oliveira e Silva (Feb. 5, 2005) |
The conjecture that all odd numbers 
are the sum of three odd primes is called the "weak" Goldbach conjecture. Vinogradov (1937ab, 1954) proved that every sufficiently large odd number is the sum of three primes (Nagell 1951, p. 66; Guy 1994), and Estermann (1938) proved that almost all even numbers are the sums of two primes. Vinogradov's original "sufficiently large" 
was subsequently reduced to 
by Chen and Wang (1989). Chen (1973, 1978) also showed that all sufficiently large even numbers are the sum of a prime and the product of at most two primes (Guy 1994, Courant and Robbins 1996).
A stronger version of the weak conjecture, namely that every odd number 
can be expressed as the sum of a prime plus twice a prime has been formulated by C. Eaton. This conjecture has been verified for 
(Corbit).
An equivalent statement of the Goldbach conjecture is that for every positive integer m, there are primes p and q such that
where 
is the totient function (e.g., Havil 2003, p. 115; Guy 2004, p. 160). (This follows immediately from 
for p prime.) Erdos and Moser have considered dropping the restriction that p and q be prime in this equation as a possibly easier way of determining if such numbers always exist (Guy 1994, p. 105).
Other variants of the Goldbach conjecture include the statements that every even number 
is the sum of two odd primes, and every integer 
the sum of exactly three distinct primes.
Let R(n) be the number of representations of an even number n as the sum of two primes. Then the "extended" Goldbach conjecture states that
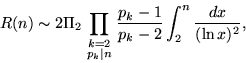
where 
is the twin primes constant (Halberstam and Richert 1974).
Chen's Theorem, de Polignac's Conjecture, Goldbach Number, Goldbach Partition, Prime Partition, Schnirelmann's Theorem, Waring's Prime Number Conjecture
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 64, 1987.
Caldwell, C. K. "Prime Links++." http://primes.utm.edu/links/theory/conjectures/Goldbach/.
Chen, J.-R. "On the Representation of a Large Even Number as the Sum of a Prime and the Product of at Most Two Primes." Sci. Sinica 16, 157-176, 1973.
Chen, J.-R. "On the Representation of a Large Even Number as the Sum of a Prime and the Product of at Most Two Primes, II." Sci. Sinica 21, 421-430, 1978.
Chen, J.-R. and Wang, T.-Z. "On the Goldbach Problem." Acta Math. Sinica 32, 702-718, 1989.
Corbit, D. sci.math posting. Nov 19, 1999.
Courant, R. and Robbins, H. What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 30-31, 1996.
Deshouillers, J.-M.; te Riele, H. J. J.; and Saouter, Y. "New Experimental Results Concerning The Goldbach Conjecture." In Algorithmic Number Theory: Proceedings of the 3rd International Symposium (ANTS-III) held at Reed College, Portland, OR, June 21-25, 1998 (Ed. J. P. Buhler). Berlin: Springer-Verlag, pp. 204-215, 1998.
Devlin, K. Mathematics: The New Golden Age, rev. ed. New York: Columbia University Press, 1999.
Dickson, L. E. "Goldbach's Empirical Theorem: Every Integer is a Sum of Two Primes." In History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Chelsea, pp. 421-424, 1952.
Doxiadis, A. Uncle Petros and Goldbach's Conjecture. Faber & Faber, 2001.
Dunham, W. Journey through Genius: The Great Theorems of Mathematics. New York: Wiley, p. 83, 1990.
Estermann, T. "On Goldbach's Problem: Proof that Almost All Even Positive Integers are Sums of Two Primes." Proc. London Math. Soc. Ser. 2 44, 307-314, 1938.
Faber and Faber. "$1,000,000 Challenge to Prove Goldbach's Conjecture." Archived at http://web.archive.org/web/20020803035741/www.faber.co.uk/faber/million_dollar.asp.
Goldbach, C. Letter to L. Euler, June 7, 1742. http://www.mathstat.dal.ca/~joerg/pic/g-letter.jpg or http://www.informatik.uni-giessen.de/staff/richstein/pic/g-letter-zoomed.jpg.
Granville, A.; van der Lune, J.; and te Riele, H. J. J. "Checking the Goldbach Conjecture on a Vector Computer." In Number Theory and Applications: Proceedings of the NATO Advanced Study Institute held in Banff, Alberta, April 27-May 5, 1988 (Ed. R. A. Mollin). Dordrecht, Netherlands: Kluwer, pp. 423-433, 1989.
Guy, R. K. "Goldbach's Conjecture." §C1 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 105-107, 1994.
Guy, R. K. Unsolved Problems in Number Theory, 3rd ed. New York: Springer-Verlag, 2004.
Halberstam, H. and Richert, H.-E. Sieve Methods. New York: Academic Press, 1974.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Hardy, G. H. and Littlewood, J. E. "Some Problems of 'Partitio Numerorum.' III. On the Expression of a Number as a Sum of Primes." Acta Math. 44, 1-70, 1923.
Hardy, G. H. and Littlewood, J. E. "Some Problems of Partitio Numerorum (V): A Further Contribution to the Study of Goldbach's Problem." Proc. London Math. Soc. Ser. 2 22, 46-56, 1924.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, p. 19, 1979.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.
Nagell, T. Introduction to Number Theory. New York: Wiley, p. 66, 1951.
Oliveira e Silva, T. "Goldbach Conjecture Verification." http://www.ieeta.pt/~tos/goldbach.html.
Oliveira e Silva, T. "Verification of the Goldbach Conjecture Up to 2*10^16." NMBRTHRY@listserv.nodak.edu mailing list. March 24, 2003. http://listserv.nodak.edu/scripts/wa.exe?A2=ind0303&L=nmbrthry&P=2394.
Oliveira e Silva, T. "Verification of the Goldbach Conjecture Up to .
Oliveira e Silva, T. "New Goldbach Conjecture Verification Limit." NMBRTHRY@listserv.nodak.edu mailing list. Feb. 5, 2005. http://listserv.nodak.edu/cgi-bin/wa.exe?A1=ind0502&L=nmbrthry#9.
Peterson, I. "Prime Conjecture Verified to New Heights." Sci. News 158, 103, Aug. 12, 2000.
Pipping, N. "Die Goldbachsche Vermutung und der Goldbach-Vinogradovsche Satz." Acta. Acad. Aboensis, Math. Phys. 11, 4-25, 1938.
Pogorzelski, H. A. "Goldbach Conjecture." J. reine angew. Math. 292, 1-12, 1977.
Richstein, J. "Verifying the Goldbach Conjecture up to 
.
Schnirelman, L. G. Uspekhi Math. Nauk 6, 3-8, 1939.
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 30-31 and 222, 1985.
Sinisalo, M. K. "Checking the Goldbach Conjecture up to 
.
Stein, M. L. and Stein, P. R. "New Experimental Results on the Goldbach Conjecture." Math. Mag. 38, 72-80, 1965a.
Stein, M. L. and Stein, P. R. "Experimental Results on Additive 2 Bases." BIT 38, 427-434, 1965b.
Vinogradov, I. M. "Representation of an Odd Number as a Sum of Three Primes." Comptes rendus (Doklady) de l'Académie des Sciences de l'U.R.S.S. 15, 169-172, 1937a.
Vinogradov, I. "Some Theorems Concerning the Theory of Primes." Recueil Math. 2, 179-195, 1937b.
Vinogradov, I. M. The Method of Trigonometrical Sums in the Theory of Numbers. London: Interscience, p. 67, 1954.
Wang, Y. (Ed.). |it Goldbach Conjecture. Singapore: World Scientific, 1984.
Woon, M. S. C. "On Partitions of Goldbach's Conjecture" 4 Oct 2000. http://arxiv.org/abs/math.GM/0010027/.
Yuan, W. Goldbach Conjecture. Singapore: World Scientific, 1984.