An irrational number for which any finite pattern of numbers occurs with the expected limiting frequency in the expansion in a given base (or all bases). For example, for a normal decimal number, each digit 0-9 would be expected to occur 1/10 of the time, each pair of digits 00-99 would be expected to occur 1/100 of the time, etc. A number that is normal in base-b is often called b-normal. A number that is b-normal for every b = 2, 3, ... is said to be absolutely normal (Bailey and Crandall 2003).
As stated by Kac (1959), "As is often the case, it is much easier to prove that an overwhelming majority of objects possess a certain property than to exhibit even one such object....It is quite difficult to exhibit a 'normal' number!" (Stoneham 1970).
If a real number 
is 
-normal, then it is also 
-normal for k and m integers (Kuipers and Niederreiter 1974, p. 72; Bailey and Crandall 2001). Furthermore, if q and r are rational with 
and is b-normal, then so is 
,
is an integer, then is also c-normal (Kuipers and Niederreiter 1974, p. 77; Bailey and Crandall 2001).
Determining if numbers are normal is an unresolved problem. It is not even known if fundamental mathematical constants such as pi (Wagon 1985, Bailey and Crandall 2003), the natural logarithm of 2 
(Bailey and Crandall 2003), Apéry's constant 
(Bailey and Crandall 2003), Pythagoras's constant 
(Bailey and Crandall 2003), and e are normal, although the first 30 million digits of 
are very uniformly distributed (Bailey 1988).
While tests of 
for n = 2, 3, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15 indicate that these square roots may be normal (Beyer et al. 1970ab), normality of these numbers has also not been proven. Strangely enough, with the exception of a number of special classed of constants (e.g., Stoneham 1973, Korobov 1990, Bailey and Crandall 2003), the only numbers known to be normal (in certain bases) are artificially constructed ones such as the Champernowne constant and the Copeland-Erdos constant. In particular, the binary Champernowne constant
 |
(1) |
(Sloane's A030190) is 2-normal (Bailey and Crandall 2001).
Bailey and Crandall (2001) showed that, subject to an unproven but reasonable hypothesis related to pseudorandom number generators, the constants ,, would be 2-normal, where is Apéry's constant. Stoneham (1973) proved that the so-called Stoneham numbers
 |
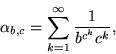(2) |
where b and c are relatively prime positive integers, are b-normal whenever c is an odd prime and p is a primitive root of 
.
is normal for all positive integers 
provided only that b and c are relatively prime.
Korobov (1990) showed that the constants
 |
(3) |
are b-normal for 
positive integers and b and c relatively prime, a result reproved using completely different techniques by Bailey and Crandall (2003). Amazingly, Korobov (1990) also gave an explicit algorithm for computing terms in the continued fraction of 
.
Bailey and Crandall (2003) also established b-normality for constants of the form 
for certain sequences of integers 
and 
.
Absolutely Normal, Champernowne Constant, Copeland-Erdos Constant, e, Equidistributed Sequence, Pi, Stoneham Number
Bailey, D. H. "The Computation of to 
Decimal Digit using Borwein's' Quartically Convergent Algorithm." Math. Comput. 50, 283-296, 1988.
Bailey, D. H. and Crandall, R. E. "On the Random Character of Fundamental Constant Expansions." Exper. Math. 10, 175-190, 2001. http://www.nersc.gov/~dhbailey/dhbpapers/baicran.pdf.
Bailey, D. H. and Crandall, R. E. "Random Generators and Normal Numbers." To appear in Exper. Math. Preprint dated Feb. 22, 2003 available at http://www.nersc.gov/~dhbailey/dhbpapers/bcnormal.pdf.
Beyer, W. A.; Metropolis, N.; and Neergaard, J. R. "Square Roots of Integers 2 to 15 in Various Bases 2 to 10: 88062 Binary Digits or Equivalent." Math. Comput. 23, 679, 1969.
Beyer, W. A.; Metropolis, N.; and Neergaard, J. R. "Statistical Study of Digits of Some Square Roots of Integers in Various Bases." Math. Comput. 24, 455-473, 1970a.
Beyer, W. A.; Metropolis, N.; and Neergaard, J. R. "The Generalized Serial Test Applied to Expansions of Some Irrational Square Roots in Various Bases." Math. Comput. 24, 745-747, 1970b.
Champernowne, D. G. "The Construction of Decimals Normal in the Scale of Ten." J. London Math. Soc. 8, 254-260, 1933.
Copeland, A. H. and Erdos, P. "Note on Normal Numbers." Bull. Amer. Math. Soc. 52, 857-860, 1946.
Gibbs, W. W. "A Digital Slice of Pi. The New Way to do Pure Math: Experimentally." Sci. Amer. 288, 23-24, May 2003.
Good, I. "Normal Recurring Decimals." J. London Math. Soc. 21, 167-169, 1946.
Good, I. J. and Gover, T. N. "The Generalized Serial Test and the Binary Expansion of .
Good, I. J. and Gover, T. N. "Corrigendum." J. Roy. Statist. Soc. Ser. A 131, 434, 1968.
Kac, M. Statistical Independence in Probability, Analysis and Number Theory. Washington, DC: Math. Assoc. Amer., 1959.
Korobov, N. "Continued Fractions of Certain Normal Numbers." Math. Zametki 47, 28-33, 1990. English translation in Math. Notes Acad. Sci. USSR 47, 128-132, 1990.
Kuipers, L. and Niederreiter, H. Uniform Distribution of Sequences. New York: Wiley, 1974.
Postnikov, A. G. "Ergodic Problems in the Theory of Congruences and of Diophantine Approximations." Proc. Steklov Inst. Math. 82, 1966.
Sloane, N. J. A. Sequences A030190 in "The On-Line Encyclopedia of Integer Sequences." http://www.research.att.com/~njas/sequences/.
Stoneham, R. "A General Arithmetic Construction of Transcendental Non-Liouville Normal Numbers from Rational Functions." Acta Arith. 16, 239-253, 1970.
Stoneham, R. "On Absolute 
-Normality in the Rational Fractions with Applications to Normal Numbers." Acta Arith. 22, 277-286, 1973.
Wagon, S. "Is Normal?" Math. Intel. 7, 65-67, 1985.
Weisstein, E. W. "Bailey and Crandall Discover a New Class of Normal Numbers." MathWorld Headline News, Oct. 4, 2001. ../topics/news/2001-10-04/normal/.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 26, 1986.