A family of operators mapping each space ![]() of modular forms onto itself. For a fixed integer k and any positive integer n, the Hecke operator
of modular forms onto itself. For a fixed integer k and any positive integer n, the Hecke operator ![]() is defined on the set
is defined on the set ![]() of entire modular forms of weight k by
of entire modular forms of weight k by
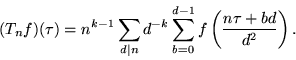 |
(1) |
For n a prime p, the operator collapses to
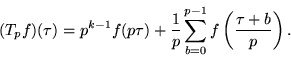 |
(2) |
If ![]() has the Fourier series
has the Fourier series
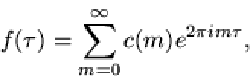 |
(3) |
then ![]() has Fourier series
has Fourier series
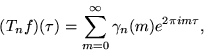 |
(4) |
where
| (5) |
(Apostol 1997, p. 121).
If ![]() ,
,
| (6) |
Any two Hecke operators T(n) and T(m) on ![]() commute with each other, and moreover
commute with each other, and moreover
| (7) |
(Apostol 1997, pp. 126-127).
Each Hecke operator ![]() has eigenforms when the dimension of
has eigenforms when the dimension of ![]() is 1, so for k = 4, 6, 8, 10, and 14, the eigenforms are the Eisenstein series
is 1, so for k = 4, 6, 8, 10, and 14, the eigenforms are the Eisenstein series ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() has eigenforms when the dimension of the set of cusp forms
has eigenforms when the dimension of the set of cusp forms ![]() is 1, so for k = 12, 16, 18, 20, 22, and 26, the eigenforms are
is 1, so for k = 12, 16, 18, 20, 22, and 26, the eigenforms are ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() is the modular discriminant of the Weierstrass elliptic function (Apostol 1997, p. 130).
is the modular discriminant of the Weierstrass elliptic function (Apostol 1997, p. 130).
![]()
![]()
![]()
Apostol, T. M. "The Hecke Operators." §6.7 in Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 120-122, 1997.
![]()