Find the ![]() array of single digits which contains the maximum possible number of primes, where allowable primes may lie along any horizontal, vertical, or diagonal line. For
array of single digits which contains the maximum possible number of primes, where allowable primes may lie along any horizontal, vertical, or diagonal line. For ![]() ,
,
giving the primes (3, 7, 13, 17, 31, 37, 41, 43, 47, 71, 73) and (3, 7, 13, 17, 19, 31, 37, 71, 73, 79, 97), respectively. For the ![]() array, 18 primes are maximal and are contained in the arrays
array, 18 primes are maximal and are contained in the arrays
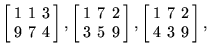 |
|||
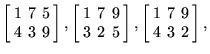 |
|||
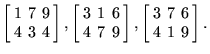 |
The best ![]() array is
array is
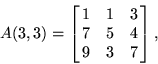
which contains 30 primes: 3, 5, 7, 11, 13, 17, 31, 37, 41, 43, 47, 53, 59, 71, 73, 79, 97, 113, 157, 179, ... (Sloane's A032529). This array was found by Rivera and Ayala and shown by Weisstein in May 1999 to be maximal and unique (modulo reflection and rotation).
The best ![]() arrays known are
arrays known are
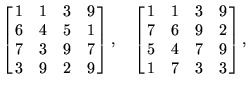 |
|
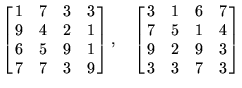 |
The best ![]() prime arrays known are
prime arrays known are
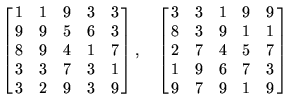 |
The best ![]() prime arrays known are
prime arrays known are
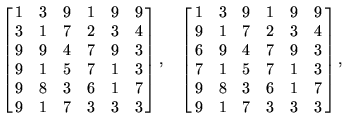 |
|
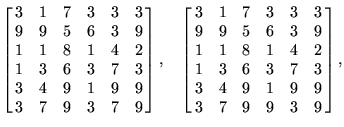 |
|
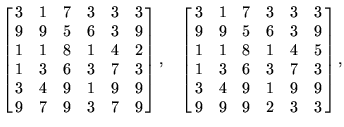 |
The best ![]() prime array known is
prime array known is

which contains 281 primes and was found by Wilfred Whiteside on April 29, 1999.
The best ![]() prime array known is
prime array known is

which contains 382 primes and was found by Wilfred Whiteside On Oct. 31, 1999.
Heuristic arguments by Rivera and Ayala suggest that the maximum possible number of primes in ![]() ,
,![]() ,
,![]() arrays are 58-63, 112-121, and 205-218, respectively.
arrays are 58-63, 112-121, and 205-218, respectively.
![]()
Array, Prime Arithmetic Progression, Prime Constellation, Prime Magic Square, Prime String
![]()
![]()
Dewdney, A. K. "Computer Recreations: How to Pan for Primes in Numerical Gravel." Sci. Amer. 259, 120-123, July 1988.
Lee, G. "Winners and Losers." Dragon User. May 1984.
Lee, G. "Gordon's Paradoxically Perplexing Primesearch Puzzle." http://www.geocities.com/MotorCity/7983/primesearch.html.
Rivera, C. "Problems & Puzzles: Puzzle 061-The Gordon Lee Puzzle." http://www.primepuzzles.net/puzzles/puzz_061.htm.
Sloane, N. J. A. Sequences A032529 in "The On-Line Encyclopedia of Integer Sequences." http://www.research.att.com/~njas/sequences/.