Number Theory > Number Theoretic Functions > General Number Theoretic Functions v
Number Theory > Number Theoretic Functions > Number Theoretic Sums v
Number Theory > Prime Numbers > Prime Number Theorem v


Explicit Formula

The so-called explicit formula


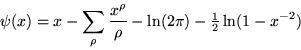
gives an explicit relation between prime numbers and Riemann zeta function zeros for x > 1 and x not a prime or prime power. Here, is the summatory Mangoldt function (also known as the second Chebyshev function), and the second sum is over all nontrivial zeros of the Riemann zeta function , i.e., those in the critical strip so (Montgomery 2001).

Chebyshe v Functions, Mangoldt Function, Prime Number Theorem, Riemann-von Mangoldt Formula, Riemann Zeta Function




References

Conrey, J. B. "The Riemann Hypothesis." Not. Amer. Math. Soc. 50, 341-353, 2003. http://www.ams.org/notices/200303/fea-conrey-web.pdf.

Davenport, H. Multiplicative Number Theory, 2nd ed. New York: Springer-Verlag, p. 104, 1980.

Havil, J. "The von Mangoldt Explicit Formula--And How It Is Used to Prove the Prime Number Theorem." §16.9 in Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 200-202, 2003.

Montgomery, H. L. "Harmonic Analysis as Found in Analytic Number Theory." In Twentieth Century Harmonic Analysis--A Celebration. Proceedings of the NATO Advanced Study Institute Held in Il Ciocco, July 2-15, 2000 (Ed. J. S. Byrnes). Dordrecht, Netherlands: Kluwer, pp. 271-293, 2001.