A cyclic number is an 
-digit integer that, when multiplied by 1, 2, 3, ..., 
,
The decimal expansions giving the first few cyclic numbers are
 |
 |
 |
(1) |
 |
|
 |
(2) |
 |
|
 |
(3) |
 |
|
 |
(4) |
(Sloane's A004042).
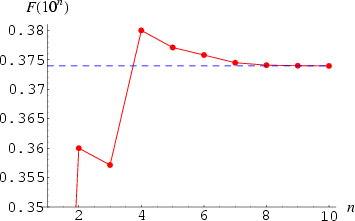
The numbers of cyclic numbers 
for n = 0, 1, 2, ... are 0, 1, 9, 60, 467, 3617, 25883, 248881, 2165288, 19016617, 170169241, ... (Sloane's A086018). It has been conjectured, but not yet proven, that an infinite number of cyclic numbers exist. In fact, the fraction of cyclic numbers out of all primes has been conjectured to be Artin's constant 
.
is 0.3739551.
When a cyclic number is multiplied by its generator, the result is a string of 9s. This is a special case of Midy's theorem.
See Yates (1973) for a table of prime period lengths for primes 
.
Artin's Constant, Decimal Expansion, Full Reptend Prime, Midy's Theorem, Unique Prime
Gardner, M. "Cyclic Numbers." Ch. 10 in Mathematical Circus: More Puzzles, Games, Paradoxes and Other Mathematical Entertainments from Scientific American. New York: Knopf, pp. 111-122, 1979.
Guttman, S. "On Cyclic Numbers." Amer. Math. Monthly 44, 159-166, 1934.
Kraitchik, M. "Cyclic Numbers." §3.7 in Mathematical Recreations. New York: W. W. Norton, pp. 75-76, 1942.
Rao, K. S. "A Note on the Recurring Period of the Reciprocal of an Odd Number." Amer. Math. Monthly 62, 484-487, 1955.
Rivera, C. "Problems & Puzzles: Puzzle 012-Period Length of 
.
Sloane, N. J. A. Sequences A001913/M4353, A004042, and A086018 in "The On-Line Encyclopedia of Integer Sequences." http://www.research.att.com/~njas/sequences/.
Yates, S. Primes with Given Period Length. Trondheim, Norway: Universitetsforlaget, 1973.