Let n be a positive nonsquare integer. Then Artin conjectured that the set S(n) of all primes for which n is a primitive root is infinite. Under the assumption of the extended Riemann hypothesis, Artin's conjecture was solved by Hooley (1967).
Let n be not an rth power for any r > 1 such the squarefree part 
of n satisfies 
(mod 4). Let 
be the set of all primes for which such an n is a primitive root. Then Artin also conjectured that the density of relative to the primes is given independently of the choice of n by 
,
 |
(1) |
(Sloane's A005596), and 
is the kth prime.
The significance of Artin's constant is more easily seen by describing it as the fraction of primes p for which 
has a maximal period repeating decimal, i.e., p is a full reptend prime (Conway and Guy 1996) corresponding to a cyclic number.
is connected with the prime zeta function P(n) by
 |
(2) |
where 
is a Lucas number (Ribenboim 1998, Gourdon and Sebah). Wrench (1961) gave 45 digits of ,
If 
and n is still restricted not to be an rth power, then the density is not itself, but a rational multiple thereof. The explicit formula for computing the density in this case is conjectured to be
 |
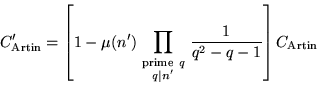(3) |
(Matthews 1976, Finch 2003), where 
is the Möbius function. Special cases can be written down explicitly for 
a prime,
 |
(4) |
or 
,
,
 |
(5) |
If n is a perfect cube (which is not a perfect square), a perfect fifth power (which is not a perfect square or perfect cube), etc., other formulas apply (Hooley 1967, Western and Miller 1968).
Artin's Conjecture, Cyclic Number, Decimal Expansion, Full Reptend Prime, Prime Products, Primitive Root, Stephens' Constant
Artin, E. Collected Papers (Ed. S. Lang and J. T. Tate). New York: Springer-Verlag, pp. viii-ix, 1965.
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, p. 169, 1996.
Finch, S. R. "Artin's Constant." §2.4 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 104-110, 2003.
Gourdon, X. and Sebah, P. "Some Constants from Number Theory." http://numbers.computation.free.fr/Constants/Miscellaneous/constantsNumTheory.html.
Hooley, C. "On Artin's Conjecture." J. reine angew. Math. 225, 209-220, 1967.
Hooley, C. Applications of Sieve Methods to the Theory of Numbers. Cambridge, England: Cambridge University Press, 1976.
Ireland, K. and Rosen, M. A Classical Introduction to Modern Number Theory, 2nd ed. New York: Springer-Verlag, 1990.
Lehmer, D. H. and Lehmer, E. "Heuristics Anyone?" In Studies in Mathematical Analysis and Related Topics: Essays in Honor of George Pólya (Ed. G. Szegö, C. Loewner, S. Bergman, M. M. Schiffer, J. Neyman, D. Gilbarg, and H. Solomon). Stanford, CA: Stanford University Press, pp. 202-210, 1962.
Lenstra, H. W. Jr. "On Artin's Conjecture and Euclid's Algorithm in Global Fields." Invent. Math. 42, 201-224, 1977.
Matthews, K. R. "A Generalization of Artin's Conjecture for Primitive Roots." Acta Arith. 29, 113-146, 1976.
Ram Murty, M. "Artin's Conjecture for Primitive Roots." Math. Intell. 10, 59-67, 1988.
Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, 1996.
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 80-83, 1993.
Sloane, N. J. A. Sequences A005596/M2608 in "The On-Line Encyclopedia of Integer Sequences." http://www.research.att.com/~njas/sequences/.
Western, A. E. and Miller, J. C. P. Tables of Indices and Primitive Roots. Cambridge, England: Cambridge University Press, pp. xxxvii-xlii, 1968.
Wrench, J. W. "Evaluation of Artin's Constant and the Twin Prime Constant." Math. Comput. 15, 396-398, 1961.