Consecutive number sequences are sequences constructed by concatenating numbers of a given type. Many of these sequences were considered by Smarandache, so they are sometimes known as Smarandache sequences.
The nth term of the consecutive integer sequence consists of the concatenation of the first n positive integers: 1, 12, 123, 1234, ... (Sloane's A007908; Smarandache 1993, Dumitrescu and Seleacu 1994, sequence 1; Mudge 1995; Stephan 1998; Wolfram 2002, p. 913). This sequence gives the digits of the Champernowne constant. The terms up to n = 9 are given by
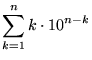 |
(1) | ||
| (2) |
Fleuren (1999) verified that the absence of primes up to n = 200, a result extended to the first
| d | n Range | Digits |
| 1 | 1-9 | n |
| 2 | 10-99 | |
| 3 | 100-999 | |
| 4 | 1000-9999 |
Therefore, the number of digits D(n) in the nth term can be written
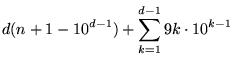 |
(3) | ||
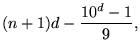 |
(4) |
where the second term is the repunit

The results of concatenating the binary representations of the first few integers are 1, 110, 11011, 11011100, 11011100101, ... (Sloane's A058935). These digit sequences are plotted above for n = 1 to 90. Interpreting the digit sequence as a binary fraction, the result is the binary Champernowne constant ![]() .
.
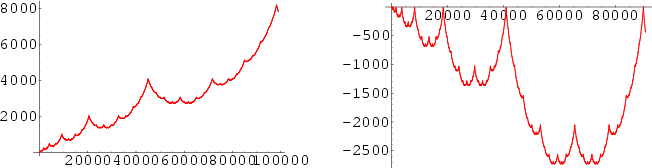
Interestingly, taking the cumulative sum ![]() where
where ![]() are the digits
are the digits ![]() gives a plot showing batrachion-like structure (left figure), and doing the same with
gives a plot showing batrachion-like structure (left figure), and doing the same with ![]() (right figure) gives structures resembling the Blancmange function (and the Hofstadter-Conway 10,000-dollar sequence).
(right figure) gives structures resembling the Blancmange function (and the Hofstadter-Conway 10,000-dollar sequence).
The nth term of the reverse integer sequence consists of the concatenation of the first n positive integers written backwards: 1, 21, 321, 4321, ... (Sloane's A000422; Smarandache 1993, Dumitrescu and Seleacu 1994, Stephan 1998). The terms up to n = 9 are given by
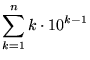 |
(5) | ||
| (6) |
The only prime in the first
There is an amazing connection between the numbers ![]() ,
,![]() ,
,
The concatenation of the first n primes gives 2, 23, 235, 2357, 235711, ... (Sloane's A019518; Smith 1996, Mudge 1997), sometimes called the Smarandache-Wellin numbers. This sequence converges to the digits of the Copeland-Erdos constant and is prime for terms 1, 2, 4, 128, 174, 342, 435, 1429, ... (Sloane's A046035; Ibstedt 1998, pp. 78-79; Crandall and Pomerance 2001, p. 72), with no others less than ![]() (Weisstein, Feb. 11, 2005). Therefore, the concatenation of all primes up to 2, 3, 7, 719, 1033, 2297, 3037, 11927, ... (Sloane's A046284) is prime.
(Weisstein, Feb. 11, 2005). Therefore, the concatenation of all primes up to 2, 3, 7, 719, 1033, 2297, 3037, 11927, ... (Sloane's A046284) is prime.
The concatenation of the first n odd numbers gives 1, 13, 135, 1357, 13579, ... (Sloane's A019519; Smith 1996, Marimutha 1997, Mudge 1997). This sequence is prime for terms 2, 10, 16, 34, 49, 2570, ... (Sloane's A046036; Weisstein, Ibstedt 1998, pp. 75-76), with no others less than ![]() (Weisstein, Feb. 11, 2005). The corresponding primes are 13, 135791113151719, 135791113151719212325272931, ... (Sloane's A048847). The 2570th term, given by 1 3 5 7...5137 5139, has 9725 digits and was discovered by Weisstein in Aug. 1998.
(Weisstein, Feb. 11, 2005). The corresponding primes are 13, 135791113151719, 135791113151719212325272931, ... (Sloane's A048847). The 2570th term, given by 1 3 5 7...5137 5139, has 9725 digits and was discovered by Weisstein in Aug. 1998.
The concatenation of the first n even numbers gives 2, 24, 246, 2468, 246810, ... (Sloane's A019520; Smith 1996; Marimutha 1997; Mudge 1997; Ibstedt 1998, pp. 77-78).
The concatenation of the first n square numbers gives 1, 14, 149, 14916, ... (Sloane's A019521; Marimutha 1997). The only prime in the first ![]() terms is the third term, 149, (Weisstein, Feb. 11, 2005).
terms is the third term, 149, (Weisstein, Feb. 11, 2005).
The concatenation of the first n cubic numbers gives 1, 18, 1827, 182764, ... (Sloane's A019522; Marimutha 1997). There are no primes in the first ![]() terms (Weisstein, Feb. 11, 2005).
terms (Weisstein, Feb. 11, 2005).
![]()
Champernowne Constant, Concatenation, Consecutive Numbers, Copeland-Erdos Constant, Cubic Number, Demlo Number, Even Number, Integer Sequence Primes, Odd Number, Smarandache Sequences, Square Number
![]()
![]()
Crandall, R. and Pomerance, C. Prime Numbers: A Computational Perspective. New York: Springer-Verlag, 2001.
Dumitrescu, C. and Seleacu, V. (Eds.). Some Notions and Questions in Number Theory. Glendale, AZ: Erhus University Press, 1994.
Fleuren, M. "Smarandache Factors and Reverse Factors." Smarandache Notions J. 10, 5-38, 1999.
Ibstedt, H. "Smarandache Concatenated Sequences." Ch. 5 in Computer Analysis of Number Sequences. Lupton, AZ: American Research Press, pp. 75-79, 1998.
Marimutha, H. "Smarandache Concatenate Type Sequences." Bull. Pure Appl. Sci. 16E, 225-226, 1997.
Mudge, M. "Top of the Class." Personal Computer World, 674-675, June 1995.
Mudge, M. "Not Numerology but Numeralogy!" Personal Computer World, 279-280, 1997.
Rivera, C. "Problems & Puzzles: Puzzle 008-Primes by Listing." http://www.primepuzzles.net/puzzles/puzz_008.htm.
Sloane, N. J. A. Sequences A000422, A007908, A019518, A019519, A019520, A019521, A019522, A046035, A046036, A046284, and A048847 in "The On-Line Encyclopedia of Integer Sequences." http://www.research.att.com/~njas/sequences/.
Smarandache, F. Only Problems, Not Solutions!, 4th ed. Phoenix, AZ: Xiquan, 1993.
Smith, S. "A Set of Conjectures on Smarandache Sequences." Bull. Pure Appl. Sci. 15E, 101-107, 1996.
Stephan, R. W. "Factors and Primes in Two Smarandache Sequences." Smarandache Notions J. 9, 4-10, 1998. Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 913, 2002.