Iff p is a prime, then 
is a multiple of p, that is
 |
(1) |
This theorem was proposed by John Wilson and published by Waring (1770), although it was previously known to Leibniz 
. in 1773. Unlike Fermat's little theorem, Wilson's theorem is both necessary and sufficient for primality. For a composite number, 
except when n = 4.
A corollary to the theorem states that iff a prime p is of the form 
,
 |
(2) |
The first few primes of the form 
are p = 5, 13, 17, 29, 37, 41, ... (Sloane's A002144), corresponding to k = 1, 3, 4, 7, 9, 10, 13, 15, 18, 22, 24, 25, 27, 28, 34, 37, ... (Sloane's A005098).
Gauss's generalization of Wilson's theorem considers P(n) the product of integers that are less than or equal to and relatively prime to an integer n. For n = 1, 2, ..., the first few values are 1, 1, 2, 3, 24, 5, 720, 105, 2240, 189, ... (Sloane's A001783). Then
 |
 |
 |
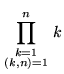(3) |
 |
 |
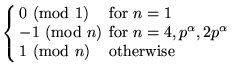(4) |
for p an odd prime. When n = 2, this reduces to
which is equivalent to 
.
are 0, -1, -1, -1, -1, -1, -1, 1, -1, -1, -1, ... (Sloane's A103131).
Fermat's Little Theorem, Prime Formulas, Wilson Prime
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 61, 1987.
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 142-143 and 168-169, 1996.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, p. 167, 2003.
Hilton, P.; Holton, D.; and Pedersen, J. Mathematical Reflections in a Room with Many Mirrors. New York: Springer-Verlag, pp. 41-42, 1997.
Nagell, T. "Wilson's Theorem and Its Generalizations." Introduction to Number Theory. New York: Wiley, pp. 99-101, 1951.
Ore, Ø. Number Theory and Its History. New York: Dover, pp. 259-261, 1988.
Séroul, R. "Wilson's Theorem." §2.9 in Programming for Mathematicians. Berlin: Springer-Verlag, pp. 16-17, 2000.
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 37-38, 1993.
Sloane, N. J. A. Sequences A001783/M0921, A002144/M3823, A005098, and A103131 in "The On-Line Encyclopedia of Integer Sequences." http://www.research.att.com/~njas/sequences/.
Waring, E. Meditationes Algebraicae. Cambridge, England: University Press, 1770.