![]()
A trinomial coefficient is a coefficient of the trinomial triangle. Following the notation of Andrews (1990),
the trinomial coefficient
![]() ,
,![]() and
and
![]() ,
,![]() in the expansion of
in the expansion of ![]() .
.
| (1) |
Equivalently, the trinomial coefficients are defined by
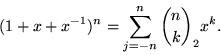 |
(2) |
The trinomial coefficients also have generating function
| (3) | |||
| (4) |
The trinomial triangle gives the triangle of trinomial coefficients,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The central column of the trinomial triangle gives the central trinomial coefficients.
The trinomial coefficient is also given by the number of permutations of n symbols, each -1, 0, or 1, which sum to
k. For example, there are seven permutations of three symbols which sum to 0, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
An alternative (but different) definition of the trinomial coefficients is as the coefficients in ![]() (Andrews 1990),
which is therefore a multinomial coefficient with k = 3, giving
(Andrews 1990),
which is therefore a multinomial coefficient with k = 3, giving
| (5) |
Trinomial coefficients have a rather sparse literature, although no less than Euler (1765) authored a 20-page paper on their properties (Andrews 1990).
The following table gives the first few columns of the trinomial triangle.
| k | Sloane | (n, k)-trinomial coefficients |
| 0 | A002426 | 1, 1, 3, 7, 19, 51, 141, 393, 1107, 3139, 8953, ... |
| 1 | A005717 | 1, 2, 6, 16, 45, 126, 357, 1016, 2907, 8350, ... |
| 2 | A014531 | 1, 3, 10, 30, 90, 266, 784, 2304, ... |
| 3 | A014532 | 1, 4, 15, 50, 161, 504, 1554, 4740, ... |
| 4 | A014533 | 1, 5, 21, 77, 266, 882, 2850, 9042, ... |
| 5 | A098470 | 1, 6, 28, 112, 414, 1452, 4917, ... |
The diagonals
![]() are summarized in the following table.
are summarized in the following table.
The trinomial coefficients satisfy an identity similar to that of the binomial coefficients, namely
| (6) |
(Andrews 1990).
Explicit formulas for
![]() are given by
are given by
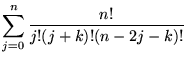 | (7) | ||
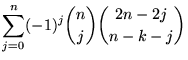 | (8) |
(Andrews 1990), which gives the closed forms
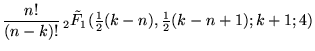 | (9) | ||
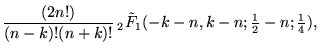 | (10) |
where
For at least n < 2000 and ![]() ,
,![]() is prime iff
is prime iff ![]() is prime only for
is prime only for ![]() ,
,
| (11) |
where ![]() is a Motzkin number, and so can only be prime for n = 2.
is a Motzkin number, and so can only be prime for n = 2.
Euler (1765) noted the pretty near-identity of central trinomial coefficients
| (12) |
where ![]() is a Fibonacci number, which holds only for
is a Fibonacci number, which holds only for ![]() (Andrews 1990). For n = 0, 1, ..., the first
few values of the left side are (Sloane's A103872), while the values on the right side are 0, 2, 2, 6, 12, 30, 72, 182,
... (Sloane's A059727). A couple of pages of Euler's works containing the near-identity was sent by D. Knuth to
R. K. Guy, who included it in his article on the strong law of small numbers (Guy 1990). Meanwhile, Guy had met
G. Andrews at the Bateman retirement conference and showed it to him. Half an hour later, Andrews came back with the
q-series identity from which Euler's near result follows. In particular, defining
(Andrews 1990). For n = 0, 1, ..., the first
few values of the left side are (Sloane's A103872), while the values on the right side are 0, 2, 2, 6, 12, 30, 72, 182,
... (Sloane's A059727). A couple of pages of Euler's works containing the near-identity was sent by D. Knuth to
R. K. Guy, who included it in his article on the strong law of small numbers (Guy 1990). Meanwhile, Guy had met
G. Andrews at the Bateman retirement conference and showed it to him. Half an hour later, Andrews came back with the
q-series identity from which Euler's near result follows. In particular, defining
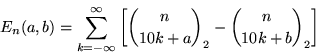 |
(13) |
gives the identities
| (14) | |||
| (15) | |||
| (16) | |||
| (17) | |||
| (18) | |||
| (19) | |||
| (20) | |||
| (21) | |||
| (22) | |||
| (23) | |||
| (24) | |||
| (25) | |||
| (26) | |||
| (27) | |||
| (28) |
(Andrews 1990). This then leads to the near-identity via
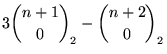 | 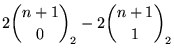 | (29) | |
| (30) | |||
| (31) |
Andrews (1990) also gave the pretty identities
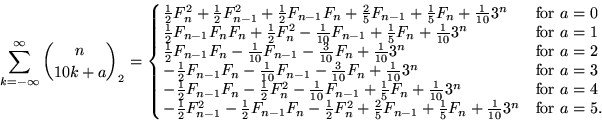 |
(32) |
![]() Binomial Coefficient, Central Trinomial Coefficient, Motzkin Number, Multinomial Coefficient, Trinomial, Trinomial Triangle
Binomial Coefficient, Central Trinomial Coefficient, Motzkin Number, Multinomial Coefficient, Trinomial, Trinomial Triangle
![]()
![]()
Andrews, G. "Euler's 'exemplum memorabile inductionis fallacis' and q-Trinomial Coefficients." J. Amer. Math. Soc. 3, 653-669, 1990.
Andrews, G. and Baxter, R. J. "Lattice Gas Generalization of the Hard Hexagon Model. III. q-Trinomial Coefficients." J. Stat. Phys. 47, 297-330, 1987.
Comtet, L. Advanced Combinatorics: The Art of Finite and Infinite Expansions, rev. enl. ed. Dordrecht, Netherlands: Reidel, p. 78, 1974.
Hoggatt, V. E. Jr., and Bicknell, M. "Diagonal Sums of Generalized Pascal Triangles." Fib. Quart. 7, 341-358 and 393, 1969.
Euler, L. "Exemplum Memorabile Inductionis Fallacis." Opera Omnia, Vol. 15. Leipzig, Germany: Teubner, 50-69, 1911.
Graham, R. L.; Knuth, D. E.; and Patashnik, O. Concrete Mathematics: A Foundation for Computer Science. Reading, MA: Addison-Wesley, p. 575, 1990.
Guy, R. K. "The Second Strong Law of Small Numbers." Math. Mag. 63, 3-20, 1990.
Henrici, P. Applied and Computational Complex Analysis, Vol. 1. New York: Wiley, p. 42, 1974.
Riordan, J. Combinatorial Identities. New York: Wiley, p. 74, 1979.
Shapiro, L. W.; Getu, S.; Woan, W.-J.; and Woodson, L. C. "The Riordan Group." Disc. Appl. Math. 34, 229-239, 1991.
Sloane, N. J. A. Sequences A000027, A000217, A000574, A002426/M2673, A005581, A005712, A005714, A005715, A005716, A005717/M1612, A014531, A014532, A014533, A027907, A059727, A098470, and A103872 in "The On-Line Encyclopedia of Integer Sequences." http://www.research.att.com/~njas/sequences/.
Warnaar, S. O. "q-Trinomial Identities." 5 Oct. 1998. http://arxiv.org/abs/math/9810018/.
![]()
![]()
|
|
|||

|

|
||