The tribonacci numbers are a generalization of the Fibonacci numbers defined by , , , and the recurrence relation

(1)

for . They represent the n = 3 case of the Fibonacci n-step numbers. The first few terms are 1, 1, 2, 4, 7, 13, 24, 44, 81, 149, ... (Sloane's A000073).

The first few prime tribonacci numbers are 2, 7, 13, 149, 19341322569415713958901, ... (Sloane's A092836), which have indices 3, 5, 6, 10, 86, 97, 214, 801, 4201, ... (Sloane's A092835).

An exact expression for the nth tribonacci number can be given explicitly by

(2)

where are the three roots of the polynomial

(3)

This can be written in slightly more concise form as

(4)

where is the nth root of the polynomial

(5)

and and are in the ordering of Mathematica's Root object.

The Tribonacci numbers can also be computed using the generating function

	(6)

Another explicit formula for is also given by

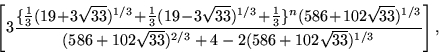(7)

where denotes the nint function (Plouffe). The first part of the numerator is related to the real root of , but determination of the denominator requires an application of the LLL algorithm.

The ratio of adjacent terms tends to the positive real root , namely 1.83929... (Sloane's A058265), sometimes known as the tribonacci constant.

Fibonacci n-Step Number, Fibonacci Number, Integer Sequence Primes, Tetranacci Number, Tribonacci Constant

search