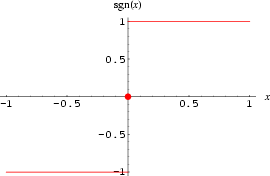
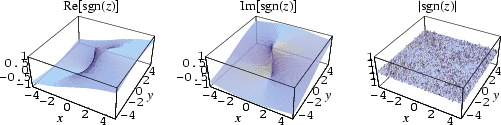
The sign of a real number, also called sgn or signum, is -1 for a negative number (i.e., one with a minus sign "![]() "), 0 for the number zero, or
"), 0 for the number zero, or ![]() for a positive number (i.e., one with a plus sign "
for a positive number (i.e., one with a plus sign "![]() "). In other words, for real x,
"). In other words, for real x,
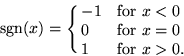
For real ![]() ,
,
| (1) |
and satisfies
| (2) |
![]() for real x can also be defined as
for real x can also be defined as
| (3) |
where H(x) is the Heaviside step function.
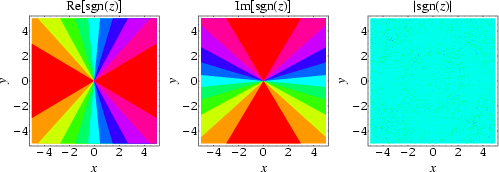
The sign function is implemented in Mathematica for real x as Sign[x]. For nonzero complex numbers, Sign[z] returns ![]() ,
,![]() is the complex modulus of z.
is the complex modulus of z.
![]() can also be interpreted as an unspecified point on the unit circle in the complex plane (Rich and Jeffrey 1996).
can also be interpreted as an unspecified point on the unit circle in the complex plane (Rich and Jeffrey 1996).
![]()
Absolute Square, Absolute Value, Complex Modulus, Heaviside Step Function, Imaginary Part, Minus Sign, Negative, Plus Sign, Positive, Ramp Function, Real Part, Sgn, Zero
![]()
![]()
Bracewell, R. "The Sign Function, ![]() .
.
Rich, A. and Jeffrey, D. "Function Evaluation on Branch Cuts." SIGSAM Bull., No. 116, 25-27, June 1996.
![]()