The prime number theorem shows that the nth prime number ![]() has the asymptotic value
has the asymptotic value
| (1) |
as ![]() (Havil 2003, p. 182). Rosser's theorem makes this a rigorous lower bound by stating that
(Havil 2003, p. 182). Rosser's theorem makes this a rigorous lower bound by stating that
| (2) |
for n > 1 (Rosser 1938). This result was subsequently improved to
| (3) |
where ![]() (Rosser and Schoenfeld 1975). The constant c was subsequently reduced to
(Rosser and Schoenfeld 1975). The constant c was subsequently reduced to ![]() (Robin 1983). Robin and Massias (1996) then showed that c = 1 was admissible for
(Robin 1983). Robin and Massias (1996) then showed that c = 1 was admissible for ![]() and
and ![]() .
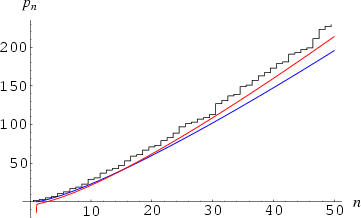
.![]() (black),
(black), ![]() (blue), and
(blue), and ![]() (red).
(red).

The difference between ![]() and
and ![]() is plotted above. The slope of the difference taken out to
is plotted above. The slope of the difference taken out to ![]() is approximately
is approximately ![]() .
.
![]()
Prime Formulas, Prime Number, Prime Number Theorem
![]()
![]()
Dusart, P. "The ![]() Prime is Greater than
Prime is Greater than ![]() for
for ![]() .
.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.
Massias, J.-P. and Robin, G. "Bornes effectives pour certaines fonctions concernant les nombres premiers." J. Théor. Nombres Bordeaux 8, 215-242, 1996.
Riesel, H. Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, pp. 56-57, 1994.
Robin, G. "Estimation de la fonction de Tschebychef ![]() sur le k-iéme nombre premier et grandes valeurs de la fonction
sur le k-iéme nombre premier et grandes valeurs de la fonction ![]() ,
,
Robin, G. "Permanence de relations de récurrence dans certains développements asymptotiques." Publ. Inst. Math., Nouv. Sér. 43, 17-25, 1988.
Rosser, J. B. "The nth Prime is Greater than ![]() .
.
Rosser, J. B. and Schoenfeld, L. "Sharper Bounds for Chebyshev Functions ![]() and
and ![]() .
.
Salvy, B. "Fast Computation of Some Asymptotic Functional Inverses." J. Symb. Comput. 17, 227-236, 1994.