A prime circle of order ![]() is a free circular permutation of the numbers from 1 to
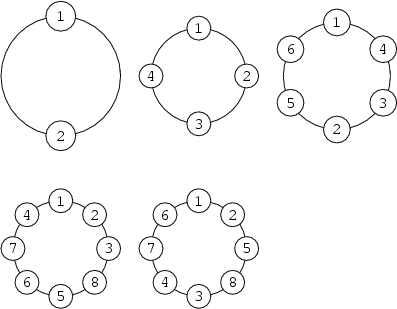
is a free circular permutation of the numbers from 1 to ![]() with adjacent pairs summing to a prime. The number of prime circles for n = 1, 2, ..., are 1, 1, 1, 2, 48, 512, ... (Sloane's A051252). The prime circles for the first few even orders are given in the table below.
with adjacent pairs summing to a prime. The number of prime circles for n = 1, 2, ..., are 1, 1, 1, 2, 48, 512, ... (Sloane's A051252). The prime circles for the first few even orders are given in the table below.
| prime circles | |
| 2 | |
| 4 | |
| 6 | |
| 8 |
![]()
![]()
![]()
Filz, A. "Problem 1046." J. Recr. Math. 14, 64, 1982.
Filz, A. "Problem 1046." J. Recr. Math. 15, 71, 1983.
Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 105-106, 1994.
Sloane, N. J. A. Sequences A051252 in "The On-Line Encyclopedia of Integer Sequences." http://www.research.att.com/~njas/sequences/.