The golden ratio ![]() can be written in terms of a nested radical in the beautiful form
can be written in terms of a nested radical in the beautiful form
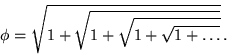 |
(1) |
This can be written recursively as
| (2) |
for ![]() ,
,![]() .
.
Paris (1987) proved ![]() approached
approached ![]() at a constant rate, namely
at a constant rate, namely
| (3) |
as ![]() ,
,
| (4) |
(Sloane's A105415) is the Paris constant.
A product formula for C is given by
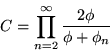 |
(5) |
(Finch 2003, p. 8).
Another formula is given by letting F(x) be the analytic solution to the functional equation
| (6) |
for ![]() ,
,![]() and
and ![]() .
.
| (7) |
(Finch 2003, p. 8).
A close approximation is ![]() ,
,
![]()
![]()
![]()
Finch, S. R. "Analysis of a Radical Expansion." §1.2.1 in Mathematical Constants. Cambridge, England: Cambridge University Press, p. 8, 2003.
Paris, R. B. "An Asymptotic Approximation Connected with the Golden Number." Amer. Math. Monthly 94, 272-278, 1987.
Plouffe, S. "The Paris Constant." http://pi.lacim.uqam.ca/piDATA/paris.txt.
Sloane, N. J. A. Sequences A105415 in "The On-Line Encyclopedia of Integer Sequences." http://www.research.att.com/~njas/sequences/.
![]()