The function 
defined by Minkowski for the purpose of mapping the rational numbers in the open interval 
into the quadratic irrational numbers of in a continuous, order-preserving manner. 
takes a number having continued fraction 
to the number
 |
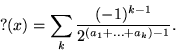(1) |
The function satisfies the following properties (Salem 1943).
- 1. 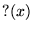is strictly increasing.
- 2. If x is rational, then 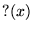is of the form
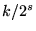, - 3. If x is a quadratic irrational number, then the continued fraction is periodic, and hence 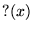is rational.
- 4. The function is purely singular (Denjoy 1938).
can also be constructed as
 |
(2) |
where 
and 
are two consecutive irreducible fractions from the Farey sequence. At the nth stage of this definition, is defined for 
values of x, and the ordinates corresponding to these values are 
for k = 0, 1, ..., 
(Salem 1943).
The function satisfies the identity
 |
(3) |
A few special values include
 |
 |
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
where
is the golden ratio.
Devil's Staircase, Farey Sequence
Conway, J. H. "Contorted Fractions." On Numbers and Games, 2nd ed. Natick, MA: A. K. Peters, pp. 82-86 (1st ed.), 2000.
Denjoy, A. "Sur une fonction réelle de Minkowski." J. Math. Pures Appl. 17, 105-155, 1938.
Girgensohn, R. "Constructing Singular Functions via Farey Fractions." J. Math. Anal. Appl. 203, 127-141, 1996.
Kinney, J. R. "Note on a Singular Function of Minkowski." Proc. Amer. Math. Soc. 11, 788-794, 1960.
Minkowski, H. "Zur Geometrie der Zahlen." In Gesammelte Abhandlungen, Vol. 2. New York: Chelsea, pp. 44-52, 1991.
Salem, R. "On Some Singular Monotone Functions which Are Strictly Increasing." Trans. Amer. Math. Soc. 53, 427-439, 1943.
Tichy, R. and Uitz, J. "An Extension of Minkowski's Singular Functions." Appl. Math. Lett. 8, 39-46, 1995.
Viader, P.; Paradis, J.; and Bibiloni, L. "A New Light on Minkowski's Function." J. Number Th. 73, 212-227, 1998.