The Fibonacci coefficient is defined by
where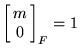 
and 
is a Fibonacci number. This coefficient satisfies
for k > 0, where 
is a Lucas number.
The triangle of Fibonacci coefficients is given by
 |
|
| 1, 1 | |
 |
|
 |
|
 |
|
 |
Fibonacci Number, Lucas Number
Benjamin, A. T. and Quinn, J. J. Proofs That Really Count: the Art of Combinatorial Proof. Washington, DC: Math. Assoc. Amer., p. 15, 2003.
Brousseau, A. Fibonacci and Related Number Theoretic Tables. San Jose, CA: Fibonacci Association, 1972.
Knuth, D. E. The Art of Computer Programming, Vol. 1: Fundamental Algorithms, 3rd ed. Reading, MA: Addison-Wesley, pp. 84 and 492, 1997.
Krot, E. "Further Developments in Finite Fibonomial Calculus." 27 Oct 2004. http://arxiv.org/abs/math.CO/0410550/.
Richardson, T. M. "The Filbert Matrix." 12 May 1999. http://arxiv.org/abs/math/9905079/.
Sloane, N. J. A. Sequences A010048 in "The On-Line Encyclopedia of Integer Sequences." http://www.research.att.com/~njas/sequences/.