The Fermat quotient for a number a and a prime base p is defined as
 |
(1) |
If 
,
 |  |  | (2) |
 | |  | (3) |
(mod p), where the modulus is taken as a fractional congruence.
The special case a = 2 is given by
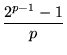 | |  | (4) |
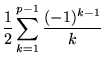|  | (5) | |
|  | (6) | |
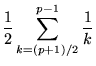|  | (7) | |
|  | (8) |
all again (mod p) where the modulus is taken as a fractional congruence,
is the digamma function,
and the last two equations hold for odd primes only.
is an integer for p a prime, with the values for p = 2, 3, 5, ... being 1, 3, 2, 5, 3, 13, 3, 17, 1, 6, ....
The quantity
is known to be zero for only two primes: the so-called
Wieferich primes 1093 and 3511 (Lehmer 1981, Crandall 1986).
Crandall, R. Projects in Scientific Computation. New York: Springer-Verlag, 1986.
Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Chelsea, p. 105, 1952.
Lehmer, D. H. "On Fermat's Quotient, Base Two." Math. Comput. 36, 289-290, 1981.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 70, 1986.
 |
|||
|
|
||