As a part of the study of Waring's problem, it is known that every positive integer is a sum of no more than 9 positive cubes (![]() ), that every "sufficiently large" integer is a sum of no more than 7 positive cubes (
), that every "sufficiently large" integer is a sum of no more than 7 positive cubes (![]() ;
;![]() ;
;
It is known that every n can be written is the form
| (1) |
An elliptic curve of the form ![]() for n an integer is known as a Mordell curve.
for n an integer is known as a Mordell curve.
The 3.1.2 equation
| (2) |
is a case of Fermat's last theorem with n = 3. In fact, this particular case was known not to have any solutions long before the general validity of Fermat's last theorem was established. Thue showed that a Diophantine equation of the form
| (3) |
for A, B, and l integers, has only finite many solutions (Hardy 1999, pp. 78-79).
Miller and Woollett (1955) and Gardiner et al. (1964) investigated integer solutions of
| (4) |
i.e., numbers representable as the sum of three (positive or negative) cubic numbers.
The general rational solution to the 3.1.3 equation
| (5) |
was found by Euler and Vieta (Dickson 1966, pp. 550-554; Hardy 1999, pp. 20-21). Hardy and Wright (1979, pp. 199-201) give a solution which can be based on the identities
| (6) | |||
| (7) |
This is equivalent to the general 3.2.2 solution found by Ramanujan ![]() (Dickson 1966, pp. 500 and 554; Berndt 1994, pp. 54 and 107; Hardy 1999, p. 11, 68, and 237). The smallest integer solutions are
(Dickson 1966, pp. 500 and 554; Berndt 1994, pp. 54 and 107; Hardy 1999, p. 11, 68, and 237). The smallest integer solutions are
| (8) | |||
| (9) | |||
| (10) | |||
| (11) | |||
| (12) | |||
| (13) | |||
| (14) | |||
| (15) | |||
| (16) | |||
| (17) | |||
| (18) | |||
| (19) | |||
| (20) | |||
| (21) | |||
| (22) | |||
| (23) | |||
| (24) | |||
| (25) | |||
| (26) | |||
| (27) | |||
| (28) | |||
| (29) |
(Fredkin 1972; Madachy 1979, pp. 124 and 141; Dutch). Other general solutions have been found by Binet (1841) and Schwering (1902), although Ramanujan's
| (30) |
3.1.4 equations include
| (31) | |||
| (32) |
3.1.5 equations include
| (33) | |||
| (34) |
and a 3.1.6 equation is given by
| (35) |
The 3.2.2 equation
| (36) |
has a known parametric solution (Dickson 1966, pp. 550-554; Guy 1994, p. 140), and 10 solutions with sum ![]() ,
,
| (37) | |||
| (38) | |||
| (39) | |||
| (40) | |||
| (41) | |||
| (42) | |||
| (43) | |||
| (44) | |||
| (45) | |||
| (46) |
(Sloane's A001235; Moreau 1898). The first number (Madachy 1979, pp. 124 and 141) in this sequence, the so-called Hardy-Ramanujan number, is associated with a story told about Ramanujan
Ramanujan ![]() gave a general solution to the 3.2.2 equation as
gave a general solution to the 3.2.2 equation as
| (47) |
where
| (48) |
(Berndt 1994, p. 107). Another form due to Ramanujan is
| |
|
| |
(49) |
Hardy and Wright (1979, Theorem 412) prove that there are numbers that are expressible as the sum of two cubes in n ways for any n (Guy 1994, pp. 140-141). The proof is constructive, providing a method for computing such numbers: given rationals numbers r and s, compute
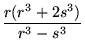 |
(50) | ||
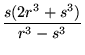 |
(51) | ||
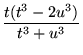 |
(52) | ||
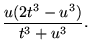 |
(53) |
Then
| (54) |
The denominators can now be cleared to produce an integer solution. If ![]() is picked to be large enough, the v and w will be positive. If
is picked to be large enough, the v and w will be positive. If ![]() is still larger, the
is still larger, the ![]() will be large enough for v and w to be used as the inputs to produce a third pair, etc. However, the resulting integers may be quite large, even for n = 2. E.g., starting with
will be large enough for v and w to be used as the inputs to produce a third pair, etc. However, the resulting integers may be quite large, even for n = 2. E.g., starting with ![]() ,
,
| (55) |
giving
| (56) | |||
| (57) |
The numbers representable in three ways as a sum of two cubes (a 3.23 equation) are
| (58) | |||
| (59) | |||
| (60) | |||
| (61) | |||
| (62) |
(Guy 1994, Sloane's A003825). Wilson (1997) found 32 numbers representable in four ways as the sum of two cubes (a 3.24 equation). The first is
| |
|
| |
(63) |
| |
|
| |
|
| |
|
| |
|
| |
(64) |
| |
|
| |
|
| |
|
| |
|
| |
(65) |
| |
|
| |
|
| |
|
| |
|
| |
(66) |
| |
|
| |
|
| |
|
| |
|
| |
(67) |
| |
|
| |
|
| |
|
| |
|
| |
(68) |
| |
|
| |
|
| |
|
| |
|
| |
(69) |
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
(70) |
A solution to the 3.4.4 equation is
| (71) |
(Madachy 1979, pp. 118 and 133).
3.6.6 equations also exist:
| |
(72) |
| |
|
| |
(73) |
In 1756-1757, Euler (1761, 1849, 1915) gave a parametric solution to
| (74) |
as
| (75) | |||
| (76) | |||
| (77) |
although relatively prime solutions require the use of fractional values of n (Dickson 1966, p. 578). To avoid this, Euler also gave the solutions
| (78) | |||
| (79) | |||
| (80) |
for ![]() ,
,
| (81) | |||
| (82) | |||
| (83) |
for
![]()
Cannonball Problem, Cubic Number, Hardy-Ramanujan Number, Multigrade Equation, Super-d Number, Taxicab Number, Trimorphic Number, Waring's Problem
![]()
![]()
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, 1994.
Berndt, B. C. and Bhargava, S. "Ramanujan--For Lowbrows." Amer. Math. Monthly 100, 645-656, 1993.
Binet, J. P. M. "Note sur une question relative à la théorie des nombres." C. R. Acad. Sci. (Paris) 12, 248-250, 1841.
Chen, S. "Equal Sums of Like Powers: On the Integer Solution of the Diophantine System." http://www.nease.net/~chin/eslp/.
Dickson, L. E. History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Chelsea, 1966.
Dutch, S. "Cubic Quartets with a, b, c < 1000." http://www.uwgb.edu/dutchs/RECMATH/Cubesums.htm.
Euler, L. Novi. Comm. Acad. Petrop. 6 (ad annos 1756-1757), p. 181, 1761.
Euler, L. Comm. Arith. Coll. 1, 207, 1849.
Euler, L. Leonhardi Euleri Opera Omnia, Ser. 1, Vol. 2. Leipzig, Germany: Teubner, p. 454, 1915.
Fredkin, E. Item 58 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, p. 23, Feb. 1972. http://www.inwap.com/pdp10/hbaker/hakmem/number.html#item58.
Gardiner, V. L.; Lazarus, R. B.; and Stein, P. R. "Solutions of the Diophantine Equation ![]() .
.
Guy, R. K. "Sums of Like Powers. Euler's Conjecture." §D1 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 139-144, 1994.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.
Koyama, K.; Tsuruoka, Y.; and Sekigawa, S. "On Searching for Solutions of the Diophantine Equation ![]() .
.
Kraus, A. "Sur l'équation ![]() .
.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, 1979.
Meyrignac, J.-C. "Computing Minimal Equal Sums Of Like Powers." http://euler.free.fr.
Miller, J. C. P. and Woollett, M. F. C. "Solutions of the Diophantine Equation ![]() .
.
Moreau, C. "Plus petit nombre égal à la somme de deux cubes de deux façons." L'Intermediaire Math. 5, 66, 1898.
Nagell, T. "The Diophantine Equation ![]() and Analogous Equations" and "Diophantine Equations of the Third Degree with an Infinity of Solutions." §65 and 66 in Introduction to Number Theory. New York: Wiley, pp. 241-248, 1951.
and Analogous Equations" and "Diophantine Equations of the Third Degree with an Infinity of Solutions." §65 and 66 in Introduction to Number Theory. New York: Wiley, pp. 241-248, 1951.
Rivera, C. "Problems & Puzzles: Puzzle 048- ![]() ,
,![]() Prime." http://www.primepuzzles.net/puzzles/puzz_048.htm.
Prime." http://www.primepuzzles.net/puzzles/puzz_048.htm.
Schwering, K. "Vereinfachte Lösungen des Eulerschen Aufgabe: ![]() .
.
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, p. 157, 1993.
Sloane, N. J. A. Sequences A001235 and A003825 in "The On-Line Encyclopedia of Integer Sequences." http://www.research.att.com/~njas/sequences/.
Wilson, D. Personal communication, Apr. 17, 1997.